№ 1. УМНОЖЕНИЕ НА ДВУЗНАЧНОЕ И ТРЕХЗНАЧНОЕ ЧИСЛО.

Умножение на двузначное и трехзначное число рассматривается на основе правила умножения числа на сумму.

а) Начинают работу с устного умножения двузначного числа на двузначное. Для ознакомления с приемом подбираются более легкие случаи, например

1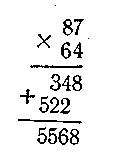 6·12=16·(10+2) = 16·10+16·2=160+32=192 . Затем надо предложить более трудный случай, например: 87·64=87·(60+4) =87·60 + 87·4

У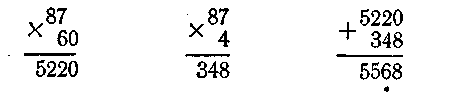 стно решить такой пример трудно, далее учитель показывает более короткую запись и дает соответствующее объяснение:

Чтобы умножить 87 на 64, надо сначала умножить 87 на 4, затем умножить 87 на 60 и полученные числа сложить. Умножаем 87 на 4: четырежды семь — 28; 8 запишем, 2 запоминаем; четырежды восемь — 32, да 2, получим 34, записываем 34. Получили 348 единиц. Теперь умножаем 87 на 60. Для этого надо 87 умножить на 6 и полученное число умножить на 10. Умножаем. Получим 5220. Сложим числа 348 и 5220. Произведение 5568. Здесь 87 и 64 — множители, 348 — первое неполное произведение, 5220 — второе неполное произведение, 5568 — окончательный результат или произведение чисел 87 и 64

После решения нескольких примеров учитель обращает внимание учащихся на особенность второго неполного произведения оно всегда оканчивается нулем. Поэтому его не пишут и второе неполное произведение начинают записывать под десятками.

Аналогично ведется объяснение умножения на трехзначное число.

Закрепление:

1) упражнения на составление плана решения, который записывают в виде выражения, но самого действия не выполняют, например: 286·374=286·4+ 286·70+286·300.

2) обратные упражнения, когда по плану решения (84·6 + 84·30) надо составить пример (84·36), а в целом можно записать следующее равенство; 84·6 + 84·30= 84·36.

3) группа упражнений, цель которых состоит в том, чтобы предупредить смешение сходных вычислительных приемов при умножении на круглые десятки и на двузначное число.

1) Учащимся предлагается рассказать способ решения пары примеров, составленных с таким расчетом, чтобы на фоне сходного ярче выступало различие приемов. Как умножить письменно 138 на 14? (Надо 138 умножить на 4, 138 умножить на 10, полученные результаты сложить: 138·14= 138·4+138·10.)Как умножить 138 на 40? (Надо 138 умножить на 4 и полученный результат умножить на 10; 138-40= 138-4-10.)

2) Упражнение, обратное первому. Если 376 умножили на 4, 376 умножили на 10 и полученные числа сложили, то на какое число умножили 376? (376·14.) Если 376 умножим на 4 и полученный результат умножим на 10, то на какое число умножили 376? (376·40.)

3) Устное и письменное решение пар примеров в одно действие: 25·12 и 25·20, а также письменное решение пар примеров в несколько действий и сравнение их. Что больше и на сколько: произведение 346·7·10 или сумма произведений 346·7+346·10?

4) Решение примеров разными способами, например

3.Деление на двузначное и трехзначное число

В основе устного деления на двузначное и трехзначное число лежит свойство деления числа на произведение:а : (b • с) = (а : b) : с

При делении числа на произведение можно разделить это число сначала на один множитель, а затем полученный результат разделить на второй множитель.

Например:240 : 30 = 240 : (3 • 10) = (240 :10): 3 = 24 : 3 = 8

2700 : 900 = 2700 : (9 • 100) = 2700 : 100 : 9 = 27 : 9 = 3

В основе письменного деления на разрядные числа лежит общий алгоритм деления на однозначное число. При ознакомлении с делением на двузначное число сначала рассматривают случаи, когда в частном получается одна цифра.

Н апример: Эту цифру частного находят приемом подбора с последующей проверкой.

Два приема подбора цифры частного:

1) Прием ориентировки на таблицу умножения однозначных чисел.

В этом случае ориентируются на последнюю цифру делителя, подбирая такую цифру частного, чтобы при умножении на нее получался результат, совпадающий с последней цифрой делимого.

Например, 384:96

В таблице умножения числа 6 только множитель 4 дает в результате умножения число, оканчивающееся на 4: 6 • 4 = 24. Проверка цифры 4 в качестве пробной цифры частного дает делимое: 96 • 4 = 384. Следовательно 384 : 96 = 4.

2) Прием замены делителя ближайшим разрядным числом.

В этом случае делитель заменяется на ближайшее разрядное число (в данном случае вместо 96 можно брать 90). В отношении разрядного числа легче найти пробную цифру частного. В данном случае деление 38 дес. на 9 дес. дает пробную цифру частного — 4. Затем ее проверяют, умножая на нее делитель. Цифра может подойти, а может и не подойти, поскольку ближайшее разрядное чис­ло берут не по правилу округления, а по принципу отбрасывания единиц. В этом случае проводится коррекция и уточненная цифра частного записывается в ответ.

Эти же приемы облегчения поиска пробной цифры частного можно использовать при делении на трехзначное число.

Например:738 : 246

Заменим число 246 ближайшим разрядным числом — это 200. 200 это 2 сот. Разделим 7 сот. на 2 сот. В частном можно пробовать цифру 3. Проверим эту пробную цифру: умножим 246 на 3, получим 738. Значит 738 : 246 = 3

Прием замены делителя на ближайшее разрядное число часто приводит к тому, что первая подобранная таким путем цифра частного не подходит и ее нужно изменять. Это происходит потому, что замена происходит не по правилам округления, а простым отбрасыванием единиц делителя.

Н апример: Заменим 47 на ближайшее разрядное число — это 40, т. е. 40 — это 4 дес. Разделим 28 дес. на 4 дес., получим 7 — это пробная циф­ра частного.

Проверяем, подходит ли цифра 7: 47 • 7 = 329 — это больше, чем 282, значит, в частном должно быть меньше, чем 7.

Проверяем, подходит ли цифра 6 : 47 • 6 = 282. Значит, 282 : 47 = 6.

Использование первого из обозначенных приемов в сочетании с приемом замены делителя на ближайшее разрядное число позволит уменьшить затраты сил и времени на поиски пробных цифр частного.

Использование общего приема округления делителя также позволит быстрее и точнее искать пробную цифру частного. В частности, в данном случае по правилам округления следовало округлять 47 до 50, а значит первая пробная цифра частного — это 6 : 50 • 6 = 300 > 282, но округление произведено с увеличением, а результат близок к делимому, значит можно пробовать 6 в качестве цифры частного.

Случаи, требующие нескольких прикидок по цифрам частного

Случай, когда при первой пробе получается число 10.

Н апример: В частном одна цифра. Прием округления, как и прием замены делителя на ближайшее разрядное число, дает в качестве делителя число 100. Первая пробная цифра частного в этом случае получается 10. Но число 10 содержит две цифры, поэтому оно не подходит.

Пробуем в качестве цифры частного 9. Проверяем: 127 • 9 = 1143 > > 1016, значит, цифра 9 не подходит.

Пробуем 8 :127 • 8= 1016. Значит 1016 : 127 = 8.

Случай, когда в частном получается не одна цифра, проще ориентироваться при подборе пробной цифры частного на первые цифры делимого и делителя.

Н апример: Первое неполное делимое — 818 десятков, значит, в частном будет две цифры — десятки и единицы.

Первая цифра делимого 8, первая цифра делителя 3, делим 8:3, можно взять по 2. Проверяем первую пробную цифру частного 341 • 2 = 682. Находим остаток 818 - 682 = 136 < 341, значит, цифра 2 подходит.

Второе неполное делимое 1364, первая цифра 1, но она на 3 не разделится. Значит, делим 13 на 3. Можно взять по 4. Проверяем вторую пробную цифру частного 341 • 4 = 1364. Значит, 4 подходит. Деление закончено.

Ответ 24. Пробная цифра частного проверяется устно, и в этом основная трудность деления на двузначное и трехзначное число.

Письменные алгоритмы умножения и деления на двузначное и трехзначное число дети изучают в конце 4 класса.

№ 9 УМНОЖЕНИЕ НА ЧИСЛА, ОКАНЧИВАЮЩИЕСЯ НУЛЯМИ. Рассмотрим приемы:

а) Прием умножения на разрядные числа:10, 100, 1000,– это связано со знанием нумерации чисел.

Вводятся подготовительные упражнения на замену круглых десятков (сотен) произведением однозначного числа и 10 (100), например: 70=7· 10, 600=6· 100.

Сначала рассматриваются устные приемы умножения на круглые десятки и сотни. Например 15*30; представим число 30 в виде произведения удобных множителей 3 и 10. Получим: 15· 30=15· (3· 10). Здесь удобнее умножить число на первый множитель — на 3, и полученный результат умножить на второй множитель — на 10. Вычислим: 15· 3=45, 45· 10 = 450. Произведение 450. Получается запись: 15· 30= 15· (3· 10) = (15· 3) · 10=450.

Учащиеся путают умножение на круглые десятки с умножением на двузначное число, и правило умножения числа на произведение с правилом умножения числа на сумму (ошибка вида 15*12=300 Ученик умножает 15 на 2 и полученный результат умножает на 10, т. е. он очевидно заменил число 12 суммой разрядных слагаемых 10+2, а далее умножал как на произведение чисел 10 и 2, т. е. на число 20). Аналогичная ошибка встречается в упражнениях на сравнение выражений: 27· 7· 10=27· 7 + 27· 10.

Для предупреждения ошибок выполняют упражнения на сравнение соответствующих приемов вычислений:

6*50=6·* (5·* 10) =6·* 5·* 10=300,

6·* 15=6* (10 + 5) =6* 10 + 6* 5=90

В первом примере второй множитель (50) заменили произведением удобных множителей. (5 и 10) и использовали правило умножения числа на произведение: умножили число 6 на первый множитель и полученное произведение умножили на второй множитель. Во втором примере множитель 15 заменили суммой разрядных слагаемых 10 и 5 и использовали правило умножения числа на сумму; умножили число 6 на первое слагаемое, потом умножили число 6 на второе слагаемое и полученные результаты сложили.

Ученики III класса путают свойства различных действий,: (6+3) · 2 = 6· 2 + 3=6+3· 2; (14 +12)+5= (14 + 5)+ (12 + 5). Путают правило прибавления числа к сумме и умножения суммы на число. В целях предупреждения ошибок в течение всего учебного года уделяют больше внимания сравнению свойств арифметических действий, изученных в I—III классах.

б) Письменное умножение на круглые десятки и сотни

546· 30 = 546· (3· 10) =546· 3· 10.

578

4

2312

Число 546 сначала умножим на 3 и полученный результат умножаем на 10. Умножаем 546 на 3; трижды шесть—18, восемь пишем, 1 запоминаем; трижды четыре—12, да 1, получится 13, три пишем, 1 запоминаем; трижды пять—15, да 1, получится 16, записываем 16, получаем 1638. Умножаем 1638 на 10, для этого приписываем к полученному числу справа один нуль. Произведение 16380.

в) Умножение на круглые сотни и тысячи выполняется аналогично умножению на круглые десятки. Особого внимания заслуживают случаи, в которых оба множителя оканчиваются нулями, например: 20·30, 400·50, 800·70, 4000·60 и т. д. При решении таких примеров учащиеся рассуждают следующим образом: чтобы умножить 300 на 50, надо 3 сотни умножить на 5, а затем полученное число умножить на 10, будет 150 сотен, или 15000. Такие примеры записываются в строчку и решаются устно.

Аналогичным образом рассуждают ученики и при письменном умножении в том случае, когда оба множителя оканчиваются нулями.

З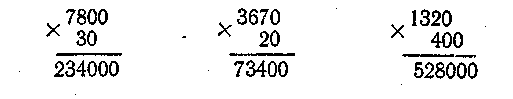 аписывать такие примеры в столбик удобнее следующим образом:

Выполняя умножение, ученики замечают, что сначала они умножили, например, число 78 или 367 на однозначное, а затем к полученному произведению приписывают столько нулей, сколько их на конце множителей. На основе этого учащиеся формулируют правило: «Если множители оканчиваются нулями, производят умножение, не обращая внимания на эти нули, а затем приписывают к произведению столько нулей, сколько их на конце обоих множителей вместе».

№ 11 ПИСЬМЕННОЕ ДЕЛЕНИЕ НА ОДНОЗНАЧНОЕ ЧИСЛО

Прием письменного деления включает операции:

- замену делимого суммой удобных слагаемых (это чаще называют выделением неполных делимых),

-деление на делитель каждого слагаемого (неполного делимого),

-сложение полученных частных.

Письменное деление всегда начинают с высших разрядов, в отличие от письменного умножения.

Этапы формирования письменного алгоритма деления:

1-й этап: рассматриваются случаи вида 794 : 2; 984 : 4 — первое неполное делимое однозначное;

2-й этап: рассматриваются случаи вида 376 : 4; 198 : 6 — первое неполное делимое двузначное;

3-й этап: рассматриваются случаи с нулями в частном (на конце или в середине);

4-й этап: рассматривается деление чисел, оканчивающихся нулями.

Описание процесса деления «в столбик», пошагово оговаривающее каждое умственное действие по выполнению подбора и проверки цифр частного, нахождения количества разделенных разрядных единиц, нахождения остатка.

Н апример: Общий алгоритм деления

1. Делю сотни: 7 сот. делю на 2, можно взять по 3 сот. В частном будет 3 сот.

Проверяю, сколько сотен разделилось: 3 сот. -2 = 6 сот. Нахожу остаток от деления сотен: 7 сот. - 6 сот. = 1 сот.

2. Делю десятки: 1 сот. = 10 дес. и еще 4 дес. — это 14 дес. 14 дес.делю на 2 — можно взять по 7. Записываю в частном 7 в разряде десятков. 7 дес. • 2 = 14 дес. Нахожу остаток: 14 дес. - 14 дес. = 0.Десятки разделились все.

3. Делю единицы — единиц 8. 8 делю на 2, можно взять по 4. Проверяю: 4 • 2 = 8. Пишу в частном 4 в разряде единиц. Единицы разделились все: 8-8 = 0. Остатка нет. Деление закончено.

Ответ: 374.

При делении вида ход рассуждений аналогичен, только первое неполное делимое — 45 десятков, поскольку 4 сотни нельзя разделить на 8 так, чтобы получить в частном сотни. Таким образом, первая значащая цифра частного в этом случае будет цифрой десятков.

Приём подбора цифр частного заключается в определении цифр в записи частного. Для этого нужно выделить первое неполное делимое и определить его десятичный состав, который и позволяет определить количество цифр частного.

Например: В случае деления 748 : 2 первое неполное делимое — 7 сотен, поскольку 7 сотен можно разделить на 2 так, чтобы в частном получились сотни. Следовательно, первой значащей цифрой частного будет цифра сотен, тогда в частном будет три цифры (сотни, десятки и единицы).

Во втором случае деления 456 : 8 первое неполное делимое — 45 десятков, следовательно первой значащей цифрой частного будет цифра десятков, тогда в частном будет две цифры (десятки и единицы).

При делении вида первое неполное делимое — 45 десятков, следовательно первой значащей цифрой частного будет цифра десятков, тогда в частном будет две цифры (десятки и единицы).

Применение этого прием при выполнении деления, приводящего к случаям получения нулей в частном.

П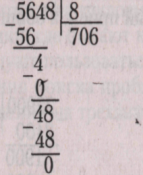 ервое неполное делимое 56 сотен (поскольку 5 тысяч нельзя разделить на 8 так, чтобы получить в частном тысячи), значит, первой цифрой частного будет цифра сотен. Следовательно, в частном будет три цифры (сотни, десятки и единицы). Данное рассуждение полезно отметить постановкой соответствующего количества точек в частном. Это предупредит распространенную в таких случаях ошибку — потерю цифры частного. При объяснении получения нуля в частном следует в речевом сопровождении компенсировать условность сокращенной записи деления в столбик: 4 десятка нельзя разделить на 8 так, чтобы в частном получились целые десятки, поэтому в разряде десятков частного ставим 0. 4 десятка — это 40 единиц, да еще 8 единиц — делим 48 на 8...

При делении чисел, оканчивающихся нулями, следует постоянно применять прием «прикидки» цифр частного, это поможет ребенку не терять нули в конце деления.

Н апример:Прием подбора цифр частного поможет ребенку при выполнении деления вида:

УМНОЖЕНИЕ МНОГОЗНАЧНОГО ЧИСЛА НА ОДНОЗНАЧНОЕ ЧИСЛО.

1) Правило умножения суммы на число учащиеся могут применить самостоятельно к устному умножению многозначных чисел на однозначное, например:

2100·3= (2000 + 100) ·3 = 2000·3+100-·3=6300

5007·4= (5000 + 7) ·4 = 5000·4 + 7·4 = 20028

Переход от устного умножения к письменному строят так, чтобы учащиеся поняли, что сущность вычислительного приема при устном и при письменном умножении на однозначное число одна и та же: используется правило умножения суммы на число, но письменное умножение начинается с низших разрядов, устное — с высших.

2) При ознакомлении с письменным умножением рассматривают пример на умножение трех- или четырехзначного числа на однозначное, где есть переходы через десяток или через сотню.

418·3. Сначала решают способом замены первого множителя суммой разрядных слагаемых и умножают сумму на число:

а) 418·3= (400+10 + 8)-3=400·3+ 10·3 + 8·3= 1200 + 30 + 24=1254

Далее решают пример, переставив разрядные слагаемые:

418·3=(8+10 + 400)·3= 8·3+ 10·3 + 400·3 = 24 +30+1200=1254

П

418

3

1254

осле этого знакомят с письменным умножением на однозначное число: показывают новую запись столбиком и дает подробное объяснение решения этого же примера. Надо умножить 418 на 3. Записываем второй множитель под единицами первого множителя. Проводим черту. Слева ставим знак умножения «X» (надо пояснить детям, что умножение обозначается не только точкой, но и таким знаком, хотя и здесь можно использовать точку). Начинаем письменное умножение с единиц. Умножаем 8 единиц на 3, получается 24 единицы. Это два десятка и 4 единицы. 4 единицы пишем под единицами, а 2 десятка запомним. 1 десяток умножим на 3, получим 3 десятка, да еще 2 десятка, получим 5 десятков. Пишем их под десятками. 4 сотни умножаем на 3, получим 12 сотен. Это 1 тысяча и 2 сотни. 2 сотни пишем под сотнями и 1 тысячу пишем на месте тысяч. Произведение 1254.

Постепенно переходят к краткому объяснению, опускается название разрядных единиц, например:

Н

578

4

2312

адо умножить 578 на 4. Умножаю 8 на 4, получится 32. Два пишу, а 3 запоминаю. 7 умножу на 4, получится 28, да 3. Всего 31; 1 пишу, а 3 запоминаю. Умножаю 5 на 4, получится 20, да 3. Всего 23; записываю 23. Произведение 2312. Можно кратко объяснить и так: четырежды восемь — тридцать два. Два пишу, 3 запоминаю. Четырежды семь — двадцать восемь и т. д.

Запись выполнят и в строчку 578·4 = 2312.

В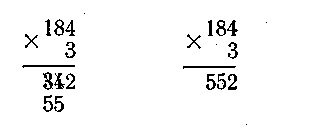 начале изучения темы учитель сообщает, что письменное умножение на однозначное число начинается с единиц, а позднее разъясняют, почему письменное умножение, начинают с низшего, а не с высшего разряда(неудобно приходится зачеркивать ранее записанные цифры) С этой целью решают пример двумя способами:

б) Рассмотрим случаи с нулями в первом множителе. Пусть надо 42300 умножить на 6.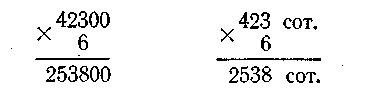

В числе 42 300 содержится 423 сотни. Умножаем 423 сотни на 6, получится 2538 сотен, или 253 800.

в) Умножение однозначного числа на многозначное, используя переместительное свойство

На данном этапе решают примеры на умножение однозначных чисел на многозначные, используя переместительное свойство умножения: 913·6, 4·2836, 7·1230 (136·9, 2836·4, 1230·7).

г) Умножение многозначных чисел, у которых есть нули в конце и середине, используя переместительное свойство

д) Умножение величин, выраженных в метрических единицах.

Примеры решают по-разному: сразу выполнить умножение или сначала заменить составное именованное число простым, выполнить действие над отвлеченными числами и затем простое число заменить составным:

9 т 438 кг 3 28т 314 кг

9 т 438 кг · 3 = 28 т 314 кг 9 т 438 3 28т 314 (кг)

№ 22. ТАБЛИЧНОЕ УМНОЖЕНИЕ

Изучение таблицы умножения является центральной задачей обучения математике во 2 и 3 классе.

К табличному умножению относят случаи умножения однозначных натуральных чисел на однозначные натуральные числа, результаты которых находят на основе конкретного смысла действия умножения (находят суммы одинаковых слагаемых).

Результаты табличного умножения в соответствии с программными требованиями к знаниям, умениям и навыкам дети должны знать наизусть. Умножение с числом нуль, умножение с числами 1 и 10 относят к особым случаям.

Первые приемы составления таблиц умножения связаны со смыслом действия умножения. Результаты этих таблиц получают последовательным сложением одинаковых слагаемых.

Н апример:

Умножение числа 2

Расположенный рядом рисунок помогает ребенку получить результат пересчетом фигурок. При небольших значениях множителей прием сосчитывания для получения табличного значения произведения вполне приемлем, и учитель им часто пользуется при получении результатов таблиц значений умножения чисел 2, 3, 4. Приведенный пример показывает, что этот прием удобен лишь при небольших значениях второго множителя.

При значении второго множителя больше 5, удобнее использовать для получения результатов табличных значений другой прием: прием прибавления к предыдущему результату.

Например:

Вычисли и запомни:

2 • 6 = 2 • 5 + 2 = ...

2 • 7 = 2 • 6 + 2 =...

В учебнике математики для 2 класса этот прием дан более пространно, и поэтому не всегда правильно понимается с точки зрения техники выполнения: 2+2+2+2+2+2 2 • 6

Аналогичным образом составляется таблица значений умножения числа 3.

Следующим приемом, на основе которого составляются таблицы значений умножения чисел, является прием перестановки множителей.

Э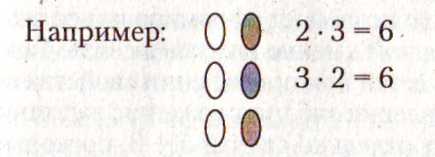 тот прием фактически является первым математическим законом относительно действия умножения в начальной школе:

От перестановки множителей произведение не меняется.

Способ знакомства детей с этим правилом (законом) обусловлен ранее введенным смыслом действия умножения. Используя предметные модели множеств, дети сосчитывают результаты группировки их элементов разными способами, убеждаясь, что результаты не меняются от изменения способов группировки.

Счет элементов рисунка (множества) парами по горизонтали совпадает со счетом элементов тройками по вертикали. Рассмотрение нескольких вариантов подобных случаев дает учителю основание произвести индуктивное обобщение (т. е. обобщение нескольких частных случаев в обобщенном правиле) о том, что перестановка множителей не меняет значение произведения.

На основе этого правила, используемого как прием счета, составляется таблица умножения на 2.

Н апример: Используя таблицу умножения числа 2, вычисли и запомни таблицу умножения на 2:

На основе этого же приема составляется таблица умножения на 3:

Составление двух первых таблиц распределяется на два урока, что соответственно увеличивает время, отведенное на их заучивание. Каждая из двух последних таблиц составляется на одном уроке, поскольку предполагается, что дети, зная исходную таблицу, не должны отдельно заучивать результаты таблиц, полученных с помощью перестановки множителей. На самом деле, многие дети учат каждую таблицу отдельно, поскольку недостаточный уровень развития гибкости мышления не позволяет им легко перестроить модель заученной схемы табличного случая в обратном порядке. При вычислении случаев вида 9 • 2 или 8 • 3 дети снова возвращаются к приему последовательного сложения, что естественно требует времени для получения результата. Такая ситуация порождается скорее всего тем, что для значительного числа детей такое разнесение во времени взаимосвязанных случаев умножения (тех, что связаны правилом перестановки множителей) не позволяет сформироваться ассоциативной цепочке, ориентированной именно на взаимосвязь.

При составлении таблицы умножения числа 5 в 3 классе, только первое произведение получают путем сложения одинаковых слагаемых: 5• 5 = 5 + 5 + 5 + 5 + 5 = 25. Остальные случаи получают приемом прибавления пяти к предыдущему результату:

5 • 6 = 5 • 5+ 5 = 30 5 • 7 = 5 • 6+ 5 = 35 5 • 8 = 5 • 7 + 5 = 40 5 • 9 = 5 • 8 + 5 = 45

Одновременно с этой таблицей составляется и взаимосвязанная с ней таблица умножения на 5: 6 • 5; 7 • 5; 8 • 5; 9 • 5.

Таблица умножения числа 6 содержит четыре случая: 6 • 6; 6 • 7; 6 • 8; 6 • 9.

Таблица умножения на 6 содержит три случая: 7 • 6; 8 • 6; 9 • 6.

Теоретический подход к подобному построению системы изуче­ния табличного умножения предполагает, что именно в таком соответствии ребенок и будет запоминать случаи табличного умножения.

Наибольшее количество случаев содержит наиболее легкая для запоминания таблица умножения числа 2, а наиболее трудная для запоминания таблица умножения числа 9 содержит всего один случай. Реально, рассматривая каждую новую «порцию» таблицы умножения, учитель обычно восстанавливает весь объем каждой таблицы (все случаи). Даже при условии, что учитель обращает внимание детей на то, что новым случаем на данном уроке является, например, только случай 9• 9,а 9• 8, 9 • 7ит. п. изучались на предыдущих уроках, большая часть детей воспринимает весь пред­ложенный объем как материал для нового заучивания. Таким образом, фактически, для многих детей таблица умножения числа 9 является самой большой и сложной (а это действительно так, если иметь в виду перечень всех случаев, который к ней относится).

Большой объем материала, требующего заучивания наизусть, сложность в образовании ассоциативных связей при запоминании взаимосвязанных случаев, необходимость достижения всеми детьми прочного запоминания всех табличных случаев наизусть в установленные программой сроки — все это делает тему изучения табличного умножения в начальных классах одной из наиболее методически сложных. В связи с этим важными являются вопросы, связанные с приемами запоминания ребенком таблицы умножения.

ПРИЕМЫ ЗАПОМИНАНИЯ ТАБЛИЦЫ УМНОЖЕНИЯ

1. Прием счета двойками, тройками, пятерками;

2. Прием последовательного сложения( данный прием связан со смыслом действия умножения как сложения одинаковых слагаемых);

3. Прием прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата)

4. Прием взаимосвязанной пары: 2 • 6 6 • 2 (перестановка множителей)

5. Прием запоминания последовательности случаев с ориентиром на возрастание второго множителя

6. Прием «порции» (активно реализован в учебнике математики для 2 и 3 классов автора Н.Б. Истоминой. Для заучивания ребенку предлагается «порция», состоящая из 2—3 случаев, но не по принципу возрастания второго множителя.Например, «порция» состоит из трех случаев: 9 • 5; 9 • 6; 9 • 7. Первым для заучивания предлагается случай 9 • 6, а от него, используя прием 3, ребенок переходит к случаям 9 • 5 и 9 • 7.В следующий раз «порция» снова содержит три случая 9 • 4; 9 • 3; 9 • 2. Здесь опорным случаем является случай 9 • 3.)

7. Прием запоминающегося случая в качестве опорного (используются легко запоминающиеся случаи: 7 • 7, 5 • 5 и т. п. Применяя затем прием прибавления или вычитания первого множителя, ребенок получает нужные результаты)

8. Прием внешней опоры (в качестве опоры используется рисунок или прямоугольная таблица чисел)

9 . Прием запоминания таблицы «с конца» (прием активно реализован в учебнике Н.Б. Истоминой. Он рекомендуется для использования при работе с детьми, плохо запоминающими большие объемы информации. В этом случае установка на запоминание ребенку дается порциями, начиная с самых сложных случав: 9 • 9,9 • 8,9 • 7. Таким образом, ребенок с ограниченным объемом запоминания запомнит сначала самые сложные случаи, а более легкие случаи таблицы чисел 2,3 и 4 он может получать приемом сложения одинаковых слагаемых или любым другим приемом)

10. Пальцевый счет при запоминании таблицы умножения

11. Мнемонические приемы при заучивании таблицы умножения (это могут быть карточки с записями табличных случаев, которые ребенок носит в кармане и просматривает при любом удобном случае (в транспорте, в очереди и т. п.).

Табличное деление

В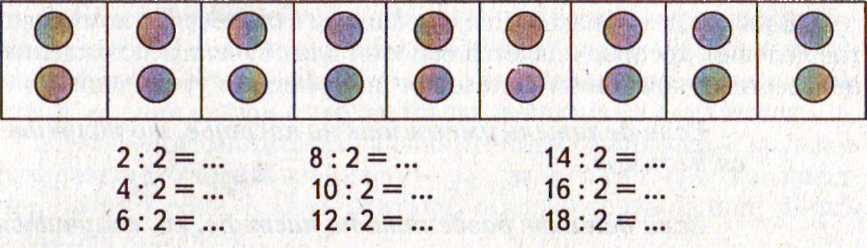 начальной школе действие деления рассматривают как действие обратное умножению. В связи с этим сначала дети знакомятся со случаями деления без остатка в пределах 100 — так называемым табличным делением. С действием деления дети знакомятся после того, как уже выучили наизусть таблицы умножения чисел 2 и 3. На основе знания этих таблиц уже на четвертом уроке после зна­комства с делением, составляется первая таблица деления на 2. Для получения ее значений используют предметный рисунок.

Значения частных в этой таблице получают подсчетом элементов рисунка на картинке.

С ледующая таблица деления — деление на 3 является последней таблицей, изучаемой во втором классе. Составляется эта таблица на основе взаимосвязи компонентов умножения с использованием правила нахождения неизвестного множителя. В связи с тем, что данное правило в явном виде предлагается детям в полной формулировке только в 3 классе, на этапе составления таблицы деления на 3 по-прежнему целесообразнее опираться на предметную модель действия (модель на фланелеграфе или рисунок).

Например: Вычисли и запомни результаты действий.

Для проверки используй рисунок:

Использование такого рисунка дает возможность составить и третий, взаимосвязанный с первыми двумя, случай деления (третий столбик). Он не относится к таблице деления на 3, но является членом взаимосвязанной тройки, который легче запоминать, ориентируясь на первые два случая. Такой прием запоминания таблицы деления (ориентир на взаимосвязанную тройку) является удобным мнемоническим приемом. Можно видеть, как дети пользуются им, реально запоминая только один прием действия умножения.

Все остальные таблицы деления изучаются в 3 классе. Поскольку умножение числа 4 и умножение на 4 также изучается уже в 3 классе, на этом году обучения прекращается практика раздельного изучения таблиц умножения и деления. Начиная с таблицы умножения числа 4, взаимосвязанные с ней таблицы деления изучают на одном уроке, сразу составляя четыре взаимосвязанных столбика случаев умножения и деления.

Например:

Используя результаты первого столбика, дети получают второй столбик перестановкой множителей, а результаты третьего и четвертого столбиков — на основе правила взаимосвязи компонентов умножения:

Если произведение разделить на один из множителей, то получится другой множитель.

Все остальные таблицы деления получают аналогичным способом.

ПРИЕМЫ ЗАПОМИНАНИЯ ТАБЛИЦЫ ДЕЛЕНИЯ

Приемы запоминания табличных случаев деления связаны со способами получения таблицы деления из соответствующих табличных случаев умножения.

1. Прием, связанный со смыслом действия деления

При небольших значениях делимого и делителя ребенок может либо произвести предметные действия для непосредственного получения результата деления, либо выполнить эти действия мысленно, либо использовать пальцевую модель.

Например: На два окна расставили поровну 10 горшков с цветами. Сколько горшков на каждом окне?

Для получения результата ребенок может воспользоваться любой из упомянутых выше моделей.

При больших значениях делимого и делителя этот прием неудобен. Например: 72 горшка с цветами расставили на 8 окон. Сколько горшков на каждом окне?

Находить результат, используя предметную модель в этом случае неудобно.

2. Прием, связанный с правилом взаимосвязи компонентов умножения и деления

В этом случае ребенок ориентируется. На запоминание взаимосвязанной тройки случаев, например:

Если ребенку удается хорошо запомнить один из этих случаев (обычно опорный — это случай умножения) или он может получить его с помощью любого из приемов запоминания таблицы умноже­ния, то используя правило «если произведение разделить на один из множителей, то получится второй множитель», легко получить второй и третий табличные случаи.

№ 13 Методика изучения приема деления двузначного числа на однозначное

При изучении приёма деления двузначного числа на однозначное пользуются правилом деления суммы на число. Рассматриваются группы примеров:

1) 46: 2 = "(40 + 6) : 2=40: 2 +-'6: 2=20 + 3=23 (делимое заменять суммой разрядных слагаемых)

2) 50 : 2= (40 + 10) : 2=40 : 2 + 10 : 2=20 + 5=25 (делимое заменяют суммой удобных слагаемых - круглые числа)

3) 72: 6= (60 +12) : 6=60: 6+ 12: 6= 10 + 2= 12 ( делимое заменяют суммой двух чисел: круглое число и двузначное)

Во всех примерах данные слагаемые будут удобными , если при делении их на данный делитель получаются разрядные слагаемые частного.

В подготовительный период используют упражнения: выделите круглые числа до 100, которые делятся на 2 (10, 20, 40, 60, 80), на 3 (30, 60, 90), на 4 (40, 80) и т. д.; представьте разными способами числа в виде суммы двух слагаемых, каждое из которых делится на данное число без остатка: 24 можно заменить суммой, каждое слагаемое которой делится на 2: 20 + 4, 12 + 12, 10+14 и т. д.; решать разными способами примеры вида: (18 + 45) : 9.

После подготовительной работы рассматриваются примеры трёх групп, при этом обращают большое внимание замене делимого суммой удобных слагаемых и выбору самого удобного способа:

42 : 3= (30+12) : 3=30 : 3+12: 3= 14

42:3=(27+15) :3=27: 3+15 : 3=14 42 :3= (24+1&) : 3 = 24: 3+18:3=14

42 : 3= (36 + 6) : 3=36:3+6: 3=14 и др.

К самому удобному способу можно отнести первый способ, так как при делении удобных слагаемых (30 и 12) получаются разрядные слагаемые частного (10 + 4=14).

Трудными являются примеры вида: 96:4. В таких случаях целесообразно заменить делимое суммой удобных слагаемых, первое из которых выражает наибольшее число десятков, делящееся на делитель: 96: 4= (80+16): 4.

Знания:

1. Разрядный состав числа

2. свойство деления суммы на число

3. Деление числа, оканчивающегося на 0

4. Табличные случая деления

5. «Удобный» состав числа.

Деление с остатком.

Деление с остатком изучается во II классе после завершения работы над внетабличными случаями умножения и деления.

Работа над делением с остатком в пределах 100 расширяет знания учащихся о действии деления, создает новые условия для применения знаний табличных результатов умножения и деления, для применения вычислительных приемов внетабличного умножения и деления, а также своевременно готовит учащихся к изучению письменных приемов деления.

Особенностью деления с остатком по сравнению с известными детям действиями является тот факт, что здесь по двум данным числам — делимому и делителю — находят два числа: частное и остаток.

Дети в своем опыте неоднократно встречались со случаями деления с остатком, выполняя деление предметов (конфет, яблок, орехов и т. д.). Поэтому при изучении деления с остатком важно опираться на этот опыт детей и вместе с тем обогатить его. Полезно начать работу с решения жизненно практических задач. Например: «15 тетрадей раздай ученикам, по 2 тетради каждому. Сколько учеников получили тетради и сколько тетрадей осталось?»

Ученики раздают, раскладывают предметы и устно отвечают на поставленные вопросы.

Наряду с этими заданиями проводится работа с дидактическим материалом и с рисунками.

Делим 14 кружков по 3 кружка. Сколько раз по 3 кружка содержится в 14 кружках? (4 раза.) Сколько кружков остается? (2.) Вводится запись деления с остатком: 14:3=4 (ост. 2). Ученики решают несколько аналогичных примеров и задач, используя предметы или рисунки. Возьмем задачу:" «Мама принесла 11 яблок и раздала их детям, по 2 яблока каждому. Сколько детей получили эти яблоки и сколько яблок осталось?» Ученики решают задачу с помощью кружков .

Решение и ответ задачи записываются следующим образом-11:2=5 (ост. 1).

Ответ: 5 детей и остается 1 яблоко.

Затем раскрывается соотношение между делителем и остатком, т. е. ученики устанавливают: если при делении получается остаток, то он всегда меньше делителя. Для этого сначала решаются примеры на деление последовательных чисел на 2, затем на 3 (4, 5). Например:

10:2=5 12:3 = 4 16:4 = 4 11:2=5(ост.1) 13:3 = 4 (ост. 1) 17:4 = 4(ост 1) 12:2=6 14:3 = 4(ост. 2) 18:4 = 4 (ост. 2)

13:2=6(ост.1) 15:3 = 5 19:4 = 4 (ост. 3)

Учащиеся сравнивают остаток с делителем и замечают, что при делении на 2 в остатке получается только число 1 и не может быть 2 (3, 4 и т. д.). Точно так же выясняется, что при делении на 3 остатком может быть число 1 или 2, при делении на 4 — только числа 1, 2, 3 и т. д. Сравнив остаток и делитель, дети делают вывод, что остаток всегда меньше делителя.

Чтобы соотношение это было усвоено, целесообразно предлагать упражнения, аналогичные следующим:

Какие числа могут получиться в остатке при делении на 5, 7, 10? Сколько различных остатков может быть при делении на 8, 11, 14? Какой наибольший остаток может быть получен при делении на 9, 15, 18? Может ли при делении на 7 получиться в остатке 8, 3, 10?

Для подготовки учащихся к усвоению приема деления с остатком полезно предлагать следующие задания:

Какие числа от 6 до 60 делятся без остатка на б, 7, 9? Какое ближайшее к 47 (52, 61) меньшее число делится без остатка на 8, 9, 6?

Раскрывая общий прием деления с остатком, лучше брать примеры парами: один из них на деление без остатка, а другой 'на деление с остатком, но примеры должны иметь одинаковые делители и частные.

Далее решаются примеры на деление с остатком без примера-помощника. -Пусть надо 37 разделить на 8. Ученик должен усвоить следующее рассуждение: «37 на 8 без остатка не делится. Самое большое число, которое меньше, чем 37, и делится на 8 без остатка, 32. 32 разделить на 8, получится 4; из 37 вычтем 32, получится 5, в остатке 5. Значит, 37 разделить на 8, получится 4 и в остатке 5».

Навык деления с остатком вырабатывается в результате тренировки, поэтому надо больше включать примеров на деление с остатком как в устные упражнения, так и в письменные работы.

Выполняя деление с остатком, учащиеся иногда получают остаток больше делителя, например: 47:5=8 (ост. 7). Чтобы предупредить такие ошибки, полезно предлагать детям неверно решенные примеры, пусть они найдут ошибку, объяснят причину ее появления и решат пример правильно.

ПАМЯТКА

1. подбери число, близкое к делимому, которое меньше его и делится без остатка;

2. раздели это число;

3. найди остаток;

4. проверь остаток, меньше ли делителя;

5. запиши пример

Во II и III классах надо как можно больше включать разнообразных упражнений на все изученные случаи умножения и деления: примеры в одно и несколько действий, сравнение выражений, заполнение таблиц, решение уравнений и т.д.

№ 14. Понятие составная задача.

Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к разбиению ее на ряд простых задач и последовательному их решению. Таким образом, для решения составной задачи надо установить ряд связей между данными и искомым, в соответствии с которыми выбрать, а затем выполнить арифметические действия.

В решении составной задачи появилось существенно новое сравнительно с решением простой задачи: здесь устанавливается не одна связь, а несколько, в соответствии с которыми выбираются арифметические действия. Поэтому проводится специальная работа по ознакомлению детей с составной задачей, а также по формированию у них умений решать составные задачи.

Подготовительная работа к ознакомлению с составными задачами должна помочь учащимся уяснить основное отличие составной задачи от простой —ее нельзя решить сразу, т. е. одним действием, а для решения надо вычленить простые задачи, установив соответствующие связи между данными и искомым. С этой целью предусматриваются специальные Упражнения: