Дискретность состояний микрообъектов. Постулаты Бора, опыты Франка и Герца, опыты Штерна и Герлаха

Для объяснения закономерностей в линейчатых спектрах Бор объединил планетарную модель атома Резерфорда с гипотезой Планка о квантовой природе света. Теория атома Бора основывается на двух постулатах:

Первый постулат Бора (постулат стационарных состояний): атомная система может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенное (дискретное) значение энергии E_n. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. В стационарных состояниях атом не излучает

Правило квантования орбит Бора утверждает: в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию

m_eυr_n = nh (n =1, 2, 3, …) ,

где m_e — масса электрона, υ — его скорость на n -й орбите радиуса r_n , h = h/ (2π ).

n - главное квантовое число, которое определяет энергетические уровни электрона в атоме.

Второй постулат Бора (правило частот): при переходе атома из одного состояния в другое испускается или поглощается один фотон с энергией

hν = E_n − E_m ,

равной разности энергий соответствующих стационарных состояний.

Набор всевозможных дискретных частот квантовых переходов:

hν = E_n − E_m

определяет линейчатый спектр атома.

Э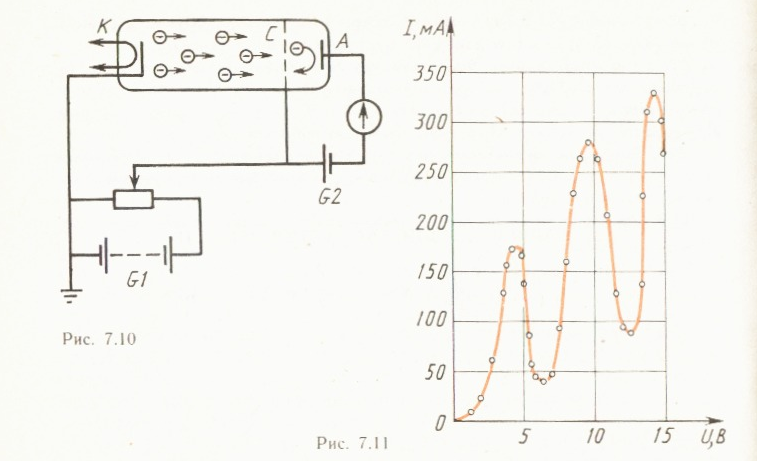 кспериментально существование в атомах стационарных состояний было доказано в опытах Франка и Герца.

Э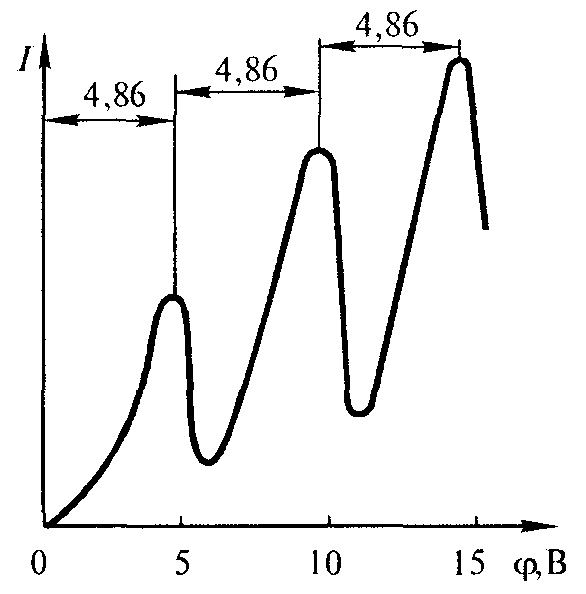 лектроны, эмитированные катодом K , разгоняются в области 1 под действием ускоряющей разности потенциалов ϕ между катодом и сеткой C1 . В области 2 электроны проходят через пары ртути и достигают анода A. Первое возбужденное состояние атома ртути имеет энергию 4,86 эВ. При увеличении ускоряющего потенциала ϕ до этой величины, соударения электронов с атомами становятся неупругими: электрон отдает кинетичес кую энергию атому, возбуждая переход из основного энергетического состояния в первое возбужденное состояние (поглощение энергии атомами ртути) — ток в установке резко уменьшается. При дальнейшем увеличении ϕ , подобное же поведение т ока наблюдается при энергиях, кратных ΔE =4,86 эВ, когда электроны испытывают 2, 3, … неупругих соударений. Таким образом, в атоме действительно существуют стационарные состояния (подтверждение первого постулата Бора). Возбужденные атомы ртути, переходя в основное состояние, излучают кванты света с длиной волны λ = 255нм (подтверждение второго постулата Бора).

Теория Бора сыграла огромную роль в создании атомной физики, в развитии атомной и молекулярной спектроскопии, но ее внутренняя противоречивость — соединение классических и квантовых представлений — не позволили на ее основе объяснить спектры многоэлектронных атомов (даже простейшего из них — атома гелия, содержащего помимо ядра два электрона). Дальнейшее развитие теория Бора получила на основе дополнительных квантовых ограничений введением еще трех квантовых чисел.

Орбитальное (азимутальное) квантовое число l при заданном n принимает значения:

l = 0,1, 2,… (n −1)

и определяет величину момента импульса (механического орбитального момента) электрона в атоме:

)

Состояние электрона, обладающего различными значениями орбитального квантового числа, принято обозначать следующим образом:

l= 0 s- состояние, l= 1 p- состояние, l= 2 d- состояние,

l= 3 f- состояние. И т.д.

Кроме механического орбитального момента импульса электрон обладает и орбитальным магнитным моментом . Между ними существует связь

,

При этом существует так называемое пространственное квантование – момент импульса электрона может иметь лишь такие ориентации в пространстве, при которых проекция вектора момента импульса на направление z внешнего магнитного поля принимает квантованные значения

L_z = m .

При этом m - магнитное квантовое число при данном l принимает значения:

m = 0, ±1, ± 2,…, ± l

и определяет величину момента импульса электрона в заданном направлении.

Таким образом, вектор может принимать 2l +1 ориентаций в пространстве. Соответственно, в магнитном поле уровень с главным квантовым числом n расщепляется на 2l +1 подуровней — эффект Зеемана.

В квантовой механике квадрат модуля волновой функции определяет вероятность обнаружения электрона в единице объема. Вероятность обнаружения электрона в разных частях атома различна. Электрон при своем движении как бы "размазан" по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число m характеризует ориентацию электронного облака в пространстве.

С. Гаудсмит и Дж.Уленбек высказали предположение о том, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, - спином.

С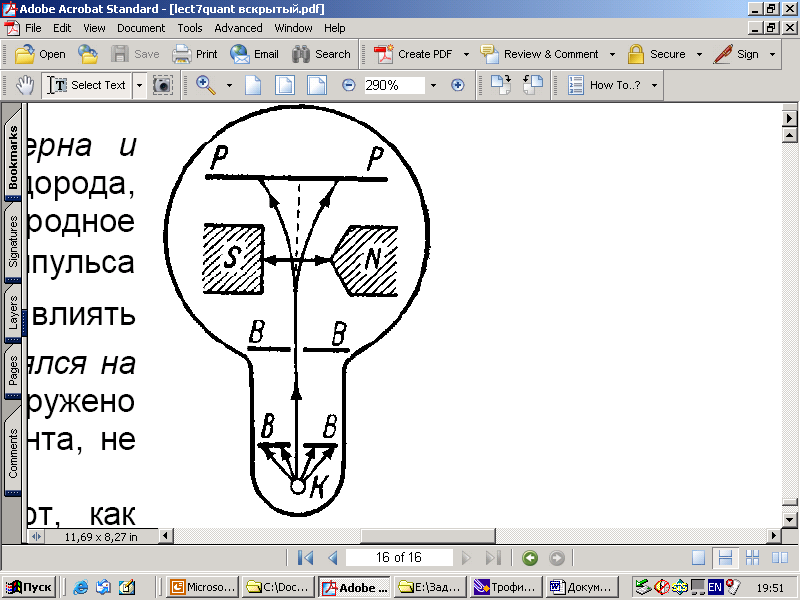 пин был обнаружен в экспериментах Штерна и Герлаха при прохождении узкого пучка атомов водорода, находящихся в s -состоянии через сильное неоднородное магнитное поле. В этом состоянии l = 0, момент импульса L0 = h l(l +1) = 0 и магнитное поле не должно было влиять на движение атомов. Однако пучок атомов расщеплялся на два пучка, следовательно, было обнаружено пространственное квантование механического момента, не связанного с орбитальным движением электрона.

Спин электрона (и всех других микрочастиц) - внутреннее неотъемлемое квантовое свойство микрочастицы: подобно тому как частицы имеют массу, а заряженные частицы — заряд, они имеют еще и спин.

Из общих выводов квантовой механики следует, что спин должен быть квантован по закону

Где s – спиновое квантовое число

Из опытов Штерна-Герлаха следует, что для спина электрона возможны две ориентации в магнитном поле, значит

При этом проекция вектора на направление внешнего магнитного поля также квантованная величина и определяется по формуле

L_sz = m_s

где - магнитное спиновое квантовое число.

Таким образом, состояние электрона в атоме определяется набором четырех квантовых чисел:

- главного n (n =1, 2, 3,…)

- орбитального l (l = 0, 1, 2, …, n −1)

- магнитного m (m = 0, ±1, ± 2,…, ± l )

- магнитного спинового m_s