§17. Пучок плоскостей

1. Пучком плоскостей называется множество всех плоскостей, проходящих через одну и ту же прямую ; прямая называется осью этого пучка. Пучок плоскостей с осью будем обозначать .

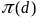Пучок плоскостей вполне определяется заданием оси . Через любую точку проходит единственная плоскость пучка .

Ось пучка плоскостей может быть задана как линия пересечения двух плоскостей пучка. Пусть известны уравнения двух различных плоскостей и пучка

: , :

в аффинной системе координат , то есть

(1)

и координаты направляющего вектора прямой удовлетворяют условию (§13 п.4):

: : (2)

Если же - координаты некоторой точки , то : ( ) (3)

Плоскость , определяемая уравнением

: (4)

принадлежит пучку тогда и только тогда, когда

, (5)

. (6)

(2),(5) . Отсюда, принимая во внимание (1) получаем , , (7) , где не равны нулю одновременно

Из уравнения (6) найдем и внесем в уравнение (4), которое принимает вид:

или в силу (7):

Используя равенства (3), получаем

(8)

Итак, произвольная плоскость пучка определяется уравнением (8), и всякое уравнение вида (8) при и , не равных нулю одновременно, определяет плоскость пучка . Следовательно, уравнение (8) есть уравнение пучка . Плоскость однозначно определяется заданием отношения в уравнении (8).

2. Отношение параллельности на множестве всех плоскостей является, очевидно, отношением эквивалентности.

Элементы фактор-множества называются пучками параллельных плоскостей. Следовательно, пучок параллельных плоскостей - это множество всех плоскостей, параллельных данной плоскости ( представителю этого пучка).

Пучок параллельных плоскостей вполне определяется заданием одной из его плоскостей

.

Уравнение (9)

определяет произвольную плоскость этого пучка тогда и только тогда, когда

(§11) и следовательно, уравнение (9) можно представить в виде

(10)

Каждому значению соответствует определенная плоскость рассматриваемого пучка параллельных плоскостей. Через любую точку проходит единственная плоскость этого пучка; она определяется уравнением (10) при

§ 18 Связка прямых и плоскостей

1.Связкой плоскостей называется множество всех плоскостей, проходящих через одну и ту же точку ; точка называется центром этой связки. Связку плоскостей с центром будем обозначать .

Связка плоскостей вполне определяется заданием ее центра . Через любую прямую , не проходящую через центр связки проходит единственная плоскость связки .

Пусть точка произвольная точка пространства, отличная от центра связки , . Всякая плоскость пучка проходит через точку и, значит, принадлежит связке . Поэтому через любую точку проходит пучок плоскостей связки . Отсюда следует, что через любую прямую проходит пучок плоскостей связки .

Зададим аффинную систему координат в пространстве, и пусть центр связки плоскостей имеет координаты . Плоскость , определяемая уравнением , проходит через точку и, значит, принадлежит связке плоскостей тогда и только тогда, когда

.

Поэтому всякая плоскость определяется уравнением вида:

(1)

и, обратно, уравнение (1), в котором не равны нулю одновременно, определяет плоскость связки .

Центр связки плоскостей может быть задан как точка пересечения трех ее плоскостей , ,

: ,

: ,

:

при условии, что

Это условие означает, что плоскости , , имеют единственную общую точку . Отсюда следует, что векторы , линейной независимы, и поэтому вектор соответствующий плоскости можно разложить по векторам базиса :

где не равны нулю одновременно. Переходя к координатам, получим :

(2)

Так как , то ( ) (3). Заменив в уравнении (1) коэффициенты по формулам (2) и использовав равенства (3), приведем уравнение (1) к виду:

( )+ ( )+

+ ( )=0 (4)

Таким образом, произвольная плоскость связки определяется уравнением (4) , и всякое уравнение вида (4) при , не равных нулю одновременно, определяет плоскость связки . Следовательно, уравнение (4) есть уравнение связки плоскостей . Плоскость однозначно определяется заданием отношений в уравнении (4).

2. Множество плоскостей, параллельных данной прямой , называется связкой плоскостей, параллельных прямой . Связка плоскостей параллельных прямой , вполне определяется заданием направляющего вектора этой прямой. Поэтому эту связку плоскостей будем обозначать через .

Плоскость , определяемая уравнением Ax+By+Cz+D=0 принадлежит связке , тогда и только тогда когда , то есть когда .

3. Связкой прямых называется множество всех прямых пространства, проходящих через одну и ту же точку ; точка называется центром этой связки. Связку прямых с центром будем обозначать .

Пусть , три прямые связки , не лежащие в одной плоскости: . Прямая , где , не равны нулю одновременно, есть произвольная прямая связки , и всякая прямая связки имеет направляющий вектор , который может быть разложен по трем некомпланарным векторам - направляющим векторам прямых из .

В качестве векторов можно взять координатные векторы аффинной системы координат .

Прямая однозначно определяется заданием отношений координат направляющего вектора прямой относительно базиса ( ), составленного из направляющих векторов трех прямых , не лежащих в одной плоскости.

Через любую точку проходит единственная прямая связки . Три прямые связки , , принадлежат одному пучку прямых тогда и только тогда, когда векторы ,

,

компланарны, то есть

4. Отношение // параллельности на множестве всех прямых пространства является отношением эквивалентности.

Элементы фактор-множества называется связками параллельных прямых или направлениями в широком смысле слова в пространстве. Значит, связка параллельных прямых - это множество всех прямых пространства, параллельных данной прямой ( представителю данной связки).

Связка параллельных прямых вполне определяется заданием какого-либо вектора ,параллельного прямым связки. Поэтому такую связку прямых будем обозначать через .

Прямая принадлежит связке тогда и только тогда, когда вектор коллинеарен вектору :

.

Через любую точку пространства пространства проходит единственная прямая связки .

Три прямые связки , , принадлежат одному пучку прямых тогда и только тогда, когда прямые в одной плоскости, и, значит, векторы , , компланарны, то есть для таких векторов выполняется условие

5. Множество называется связкой прямых и плоскостей с центром . Каждые две (различные) плоскости связки пересекаются по прямой и каждая прямая связки является осью пучка плоскостей связки . Следовательно, множество прямых по которым пересекаются плоскости связки , есть связка прямых .

И обратно, каждые две (различные) прямые связки определяют плоскость через них проходящую , и каждой плоскости принадлежит пучок прямых связки .

Таким образом, связка плоскостей порождает связку прямых и обратно.

Множество называется связкой прямых и плоскостей, параллельных прямой с направляющим вектором . Связка плоскостей порождает связку прямых и обратно.
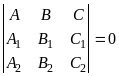