§14. Взаимное расположение прямой и плоскости.

Пусть имеем прямую d, заданную уравнениями

(1)

и плоскость П, заданную уравнением:

(2)

относительно аффинной системы координат . Будем искать общие точки прямой d и плоскости П. Для этого нужно решить систему уравнений (1) и (2). Заменяя х, у, z в уравнении (2) по формулам (1), получим:

(3)

Здесь возможны случаи:

1) (4) <=> система уравнений (1), (2) имеет единственное решение. Таким образом, условие (4) является необходимым и достаточным условием пересечения прямой d и плоскости П . В прямоугольной системе координат оно имеет простой геометрический смысл: скалярное произведение направляющего вектора прямой d и вектора нормали плоскости П отлично от нуля. Следовательно, векторы и не ортогональны.

В частности, прямая d перпендикулярна плоскости П тогда и только тогда, когда векторы и коллинеарны, т.е. когда

2. , (5)

Следовательно, уравнение (3) не имеет решений, а, значит, и система (1),(2) не имеет решения. Таким образом, условия (5) являются необходимыми и достаточными условиями того, что (прямая и плоскость параллельны).

В прямоугольной системе координат они означают, что

где .

3) (6)

Уравнение (3) удовлетворяется любым значением t, а, значит, система (1), (2) имеет бесконечное множество решений. Следовательно, условия (6) являются необходимыми и достаточными для того, чтобы прямая d принадлежала плоскости II.

В прямоугольной системе координат они означают, то что

Из соотношений (5), (6) заключаем, что

§15. Взаимное расположение двух прямых

в пространстве

Пусть имеем две прямые , каждая из которых задана точкой и направляющим вектором с координатами:

,

относительно аффинной системы координат .

Обозначим:

,

,

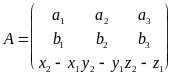1) Векторы - некомпланарны <=> rangA=3, значит detA 0. Следовательно, прямые и скрещиваются.

2) Векторы - компланарны rangA=2, т.е. det À = 0. Следовательно, прямые и лежат в одной плоскости.

а) векторы - неколлинеарны rangB = 2. Тогда прямые и пересекаются.

б) векторы и - коллинеарны, и - неколлинеарны rangB = 1, rangC = 2. При этом прямые и параллельны.

3) Векторы коллинеарны rangB = 1, rangC =1 rangА = 1. Следовательно, прямые и совпадают.

§ 16. Углы между двумя прямыми, между прямой

и плоскостью

1. Пусть каждая из прямых и задана точкой и направляющим вектором, при этом

,

, .

относительно системы координат .

Пусть прямые и заданные в пространстве, не параллельны. Возьмем произвольную точку пространства и проведем через нее прямые и соответственно параллельные прямым и . Прямые и образуют четыре угла с вершиной . Каждый из этих углов называется углом между прямыми и . Если известен один из четырех указанных углов, то легко определяются остальные три угла. Один из этих углов в точности угол между направляющими векторами этих прямых.

Таким образом, угол между прямыми и вычисляется по формуле:

Отсюда получаем условие перпендикулярности двух прямых: ( ) : .

Напомним, что две взаимно перпендикулярные прямые в пространстве могут быть как скрещивающимися, так и пересекающимися.

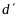2. Если прямая не параллельна плоскости , то углом между прямой и плоскостью называется острый угол между этой прямой и её ортогональной проекцией на плоскость .

Если же прямая перпендикулярна плоскости то угол между прямой и плоскостью считается равным .

Пусть уравнения , , и =0 определяют прямую и неперпендикулярную к ней плоскость относительно прямоугольной системы координат .

Обозначим через острый угол между прямой и её ортогональной проекцией на плоскость , , где - направляющий вектор прямой ,

— вектор нормали плоскости . Если угол острый , то = Если угол тупой, то =

Таким образом,

.

Поэтому

Нетрудно убедиться в том, что эта формула остается верной и в случае перпендикулярности прямой и плоскости ( когда = , а векторы и коллинераны ) .