§ 12. Расстояние от точки до плоскости. Угол между двумя плоскостями
Пусть дана плоскость своим уравнением
=0
(1)
в прямоугольной
системе координат
.
Если
(2),
(1), (2)
(*
),
где
.
Обозначим
.
(*)
,
то есть
имеет простой геометрический смысл:
(см. §
8). Он называется вектором нормали
плоскости
.
Уравнение (4) § 8 определяет в этом случае множество точек, таких, что
,
то есть плоскость
,
проходящую через точку
перпендикулярно вектору
.
Условие параллельности
вектора
плоскости
( (1) из §
9) в прямоугольной системе координат
становится очевидным: оно может быть
записано в виде
и, следовательно, означает что вектор
должен быть ортогонален вектору
плоскости
.
Всякая прямая , перпендикулярная плоскости , называется нормалью к плоскости .
В прямоугольной системе координат дана плоскость
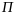уравнением
=0
и точка
не лежащая в этой плоскости. Определим
расстояние
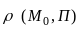от точки до плоскости
.
|
Пусть |
-
основание перпендикуляра, проведенного
из точки
к
плоскости
.
Вектор
перпендикулярен плоскости
и, следовательно, коллинеарен вектору
.
По определению скалярного произведения
=
Учитывая, что
,
=
получаем:
=
(3)
Так как
, то
и левая часть равенства (3) имеет вид
.Таким
образом, получаем
=
(4)
Используя формулу (4), вычислим расстояние
между параллельными плоскостями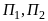
заданными в прямоугольной системе
координат
уравнениями
:
,
:
,
где
Отметим, что плоскости и действительно параллельны, так как они перпендикулярны одному и тому вектору , но не совпадают ( ).
Пусть
- произвольная точка плоскости
.
Тогда, очевидно,
=
поэтому, пользуясь формулой (4) находим,
что
=
.
Так как
.
Таким образом, получаем
=
.
(5)
4. Пусть даны две пересекающиеся плоскости и своими уравнениями
:
,
:
в прямоугольной системе координат , то есть
.
Векторы
являются
векторами нормалей плоскостей
и
соответственно.
Углом между плоскостями и называется любой из двугранных углов, образованных этими плоскостями.
Угол
равен
линейному углу одного из двугранных
углов, образованных плоскостями
и
,
поэтому для решения задачи достаточно
найти угол
|
|
2
Плоскости
и
перпендикулярны тогда и только тогда,
когда
,
то есть когда
(6)