§ 11. Взаимное расположение двух и трех плоскостей

1.Пусть даны две плоскости П₁ и П₂ своими уравнениями:

(1)

(2)

в аффинной системе координат .

Координаты х,у,z точки являются решением системы уравнений (1), (2). Поэтому вопрос о взаимном расположении плоскостей П₁ и П₂ сводится к исследованию системы линейных уравнений (1), (2). Обозначим: , .

Ясно, что , причем по теореме Кронекера-Капелли система уравнений (1) и (2) совместна тогда и только тогда, когда . Таким образом, плоскости П₁ и П₂ имеют хотя бы одну общую точку тогда и только тогда, когда .

Возможны следующие случаи:

1. . Тогда система уравнений (1) и (2) совместна и имеет бесчисленное множество решений (n = 3). Коэффициенты А₁ ,В₁ ,С₁ , D₁ уравнения (1) пропорциональны коэффициентам А₂ ,В₂ ,С₂ , D₂ уравнения (2) и уравнения (1) и (2) равносильны: А₂ =аА₁, В₂ =аВ₁, С₂ =аС₁, D₂ =аD₁. Отсюда заключаем, что каждая точка одной из плоскостей П₁ и П₂ принадлежит другой, и поэтому плоскости П₁ и П₂ совпадают. Это надо понимать так, что два уравнения (1) и (2) определяют одну и ту же плоскость.

Пусть плоскости П₁ и П₂ совпадают. Тогда уравнения (1) и (2) эквивалентны: r'=1 (r=1).

2) r'=2, r=1. По теореме Кронекера-Капелли система (1) и (2) несовместна. Тогда плоскости П₁ и П₂ не имеют общих точек, т.е. параллельны.

3) r' = 2, r = 2. Система уравнений (1) и (2) совместна и поэтому плоскости П₁ и П₂ имеют бесконечное множество общих точек (n=3). Тогда плоскости П₁ и П₂ различны ( они не могут совпасть, так как ).

Если - одно из решений системы (1) и (2), то эта система равносильна системе уравнений:

Общее решение этой системы имеет вид:

, , .

, , (3)

Уравнения (3) являются параметрическими уравнениями прямой . Направляющий вектор прямой d имеет координаты:

(определенные с точностью до общего множителя )(§13)

Таким образом, плоскости П₁ и П₂ имеют общую прямую, т.е. пересекаются.

2. Пусть даны три плоскости: П₁ и П₂, определяемые уравнениями (1) и (2) соответственно, и П₃, определяемая уравнением: (4) относительно аффинной системы координат . Вопрос о взаимном расположении этих плоскостей сводится к исследованию системы линейных уравнений (1), (2), (4). Введем обозначения:

,

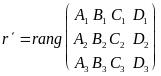, . Возможны случаи:

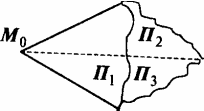
1) r'=r=3. Тогда система уравнений (1), (2), (4) имеет единственное решение, следовательно, плоскости П₁ и П₂ , П₃ имеют единственную общую точку М₀ , (см.рис.1);

рис.1

рис.2

2) r' = 3, r = 2. Система уравнений (1), (2), (4) не имеет решений, значит плоскости П₁ и П₂ , П₃ не имеют общей точки.

Так как r = 2, то по крайней мере одно из чисел (а значит и ) равно 2 и поэтому по крайней мере две плоскости из П₁ , П₂ , П₃ пересекаются. При этом третья плоскость не имеет общих точек с линией пересечения первых двух плоскостей, так как система уравнений (1), (2), (4) несовместна. Здесь возможны два случая:

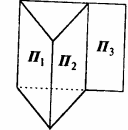
а) Каждая пара плоскостей П₁ , П₂ , П₃ пересекаются (все =2), ( см.рис.2)

б) Две плоскости из трех параллельны (не имеют общих точек). Если, например, , то плоскость П₂ пересекает плоскости П₁ и П₃ , причем П₁ //П₃ ,

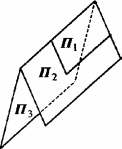
3) r'=r=2. Система уравнении (1), (2), (4) имеет бесконечное множество решений. Значит, плоскости П₁ , П₂ , П₃ имеют общие точки. В этом случае система уравнений (1), (2), (4) содержит лишь два независимых уравнения, определяющих пару пересекающих плоскостей; третье уравнение - следствие двух указанных и, значит, определяемая им плоскость проходит через линию пересечения этих двух плоскостей.

а) (см.рис.3.)

рис.3

рис.4

б) (плоскости П₁ и П₂ совпадают, плоскости П₁ и П₃ пересекаются), см. рис.4.

4) r' = 2, r = 1. Система уравнений (1), (2), (4) не имеет решений, значит плоскости П₁ , П₂ , П₃, не имеют общей точки.

а) все , = 2. Плоскости П₁ , П₂ , П₃, параллельны.

б) все , но по крайней мере одно из чисел равно 2

Cледовательно, из трех плоскостей П₁ , П₂ , П₃, по крайней мере две плоскости параллельны (не имеют общих точек), третья плоскость может совпадать с одной из параллельных плоскостей.

5) r'=r=1. Система уравнений (1), (2), (4) имеет бесконечное множество решений, значит, плоскости П₁ , П₂ , П₃ имеют общие точки. В этом случае система уравнений (1), (2), (4) содержит лишь одно независимое уравнение, два других - его следствия. Следовательно, плоскости П₁ , П₂ , П₃ совпадают.