- •Глава 2. Плоскости и прямые
- •§ 8. Различные способы задания плоскости
- •§ 9. Лемма о параллельности вектора и плоскости.
- •§ 10. Геометрический смысл знака трехчлена
- •§ 11. Взаимное расположение двух и трех плоскостей
- •§ 12. Расстояние от точки до плоскости. Угол между двумя плоскостями
- •§ 13. Различные способы задания прямой
- •2. Если , то исключая из уравнений (2), получим (3).
- •§14. Взаимное расположение прямой и плоскости.
- •§15. Взаимное расположение двух прямых
- •§ 16. Углы между двумя прямыми, между прямой
- •§17. Пучок плоскостей
- •§ 18 Связка прямых и плоскостей
- •Литература
Глава 2. Плоскости и прямые
§ 8. Различные способы задания плоскости
Вектор
![]() называется параллельным плоскости
называется параллельным плоскости
![]()
![]() ,
если
,
если
![]() /
/
![]() .
.
1. Пусть
- какая-либо плоскость в пространстве,
точка
![]() - некоторая точка этой плоскости, а
векторы
- некоторая точка этой плоскости, а
векторы
![]() - неколлинеарны и параллельны плоскости
.
- неколлинеарны и параллельны плоскости
.
Точка
![]()
![]() когда векторы
когда векторы
![]() ,
компланарны, т.е.
,
компланарны, т.е.
![]()
![]() (,
(,
![]() )
(1)
)
(1)
|
Таким образом,
чтобы задать плоскость
|
![]() ,
заданную точкой
и векторами
,
заданную точкой
и векторами
![]() и
,
будем обозначать:
и
,
будем обозначать:
![]()
Формула (1)
устанавливает взаимно однозначное
соответствие между точками плоскости
и упорядоченными парами чисел
![]() .
Из определения координат точки на
плоскости следует, что параметры ,
являются координатами точки
.
Из определения координат точки на
плоскости следует, что параметры ,
являются координатами точки
![]() относительно аффинной системы координат
относительно аффинной системы координат
![]() на плоскости
.
на плоскости
.
Пусть
![]() какая-либо аффинная система в пространстве
и относительно неё точки
какая-либо аффинная система в пространстве
и относительно неё точки
![]() и
и
![]() имеют
координаты:
имеют
координаты:
![]() ,
,
![]() Разложим векторы
Разложим векторы
![]() и
по
векторам базиса
и
по
векторам базиса
![]() :
:
![]() ,
,
![]()
![]()
Так как векторы и не коллинеарны, то
rang
![]() .
(*)
.
(*)
Сравнивая одноимённые координаты векторов в формуле (1), получим:
 (2)
(2)
Обратно, (2)![]() (1).
Таким образом, уравнения (2) определяют
плоскость
в пространстве. Они называются
параметрическими
уравнениями
плоскости.
(1).
Таким образом, уравнения (2) определяют
плоскость
в пространстве. Они называются
параметрическими
уравнениями
плоскости.
2. Из формулы (1)
следует, что определитель системы
векторов
![]() относительно базиса
равен нулю
относительно базиса
равен нулю
![]()
т.е.
 .
(3)
.
(3)
 ,
(4)
,
(4)
где
![]()
![]()
![]() .
.
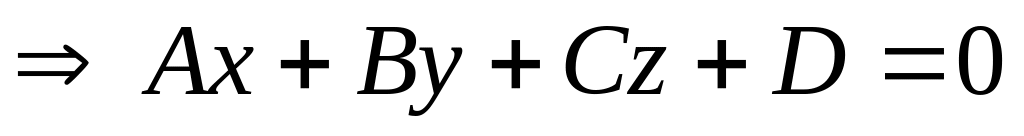 ,
где
,
где
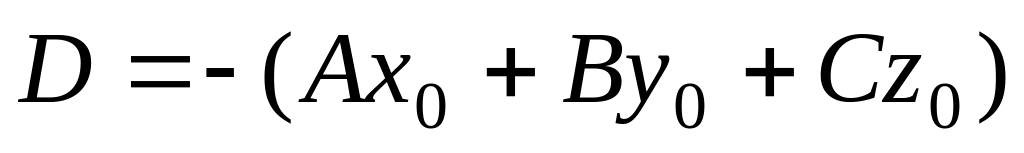 .
(5)
.
(5)
Уравнение (5) первой степени, так как в силу условия (*) по крайней мере одно из чисел А,В,С отлично от нуля. Следовательно, всякая плоскость определяется уравнением первой степени относительно аффинной системы координат в пространстве.
Справедливо и
обратное утверждение: всякое уравнение
(5) первой степени определяет некоторую
плоскость в пространстве, если задана
аффинная система координат
![]() .
.
Так как уравнение
(5) первой степени, то по крайней мере
одно из чисел А,В,С
отлично от нуля. Пусть А![]() 0.
Тогда уравнение (5) можно представить в
виде:
0.
Тогда уравнение (5) можно представить в
виде:
![]() .
.
Обозначив
![]()
![]() будем иметь:
будем иметь:
![]() ,
,
![]()
![]()
причём ранг матрицы
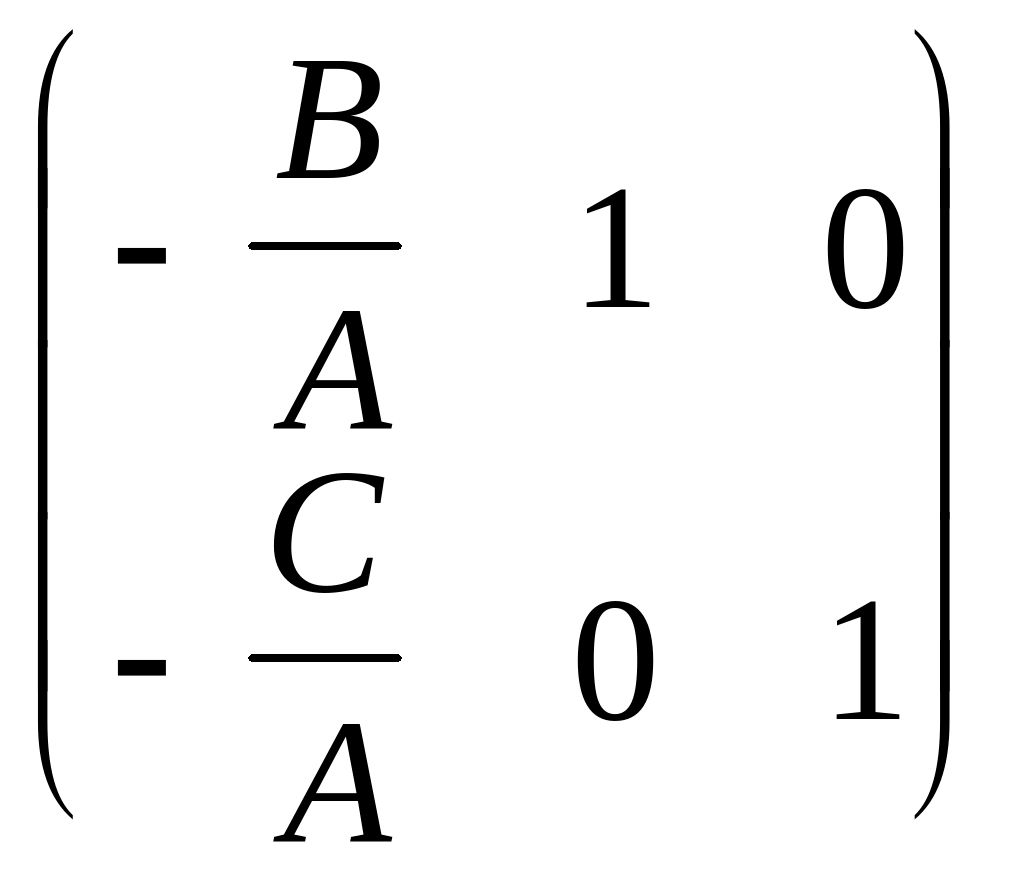 ,
,
составленный из
коэффициентов при
![]() и
и
![]() в системе
,
равен двум. Следовательно, уравнения
,
а значит, и уравнение (5) определяют
плоскость
в системе
,
равен двум. Следовательно, уравнения
,
а значит, и уравнение (5) определяют
плоскость
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
■
.
■
Уравнение (5)
называется общим
уравнением
плоскости
![]() Уравнения
являются параметрическими уравнениями
той же плоскости
(при
Уравнения
являются параметрическими уравнениями
той же плоскости
(при
![]() ).
).
3. Плоскость
будет определена, если задать три её
точки
![]() не лежащие на одной прямой:
не лежащие на одной прямой:![]() .
.
Пусть в аффинной
системе координат
точки
![]() имеют координаты:
имеют координаты:
![]() ,
,
![]() ,
,
![]() .
Тогда плоскость
определяется уравнением:
.
Тогда плоскость
определяется уравнением:
![]()
или в координатной форме:
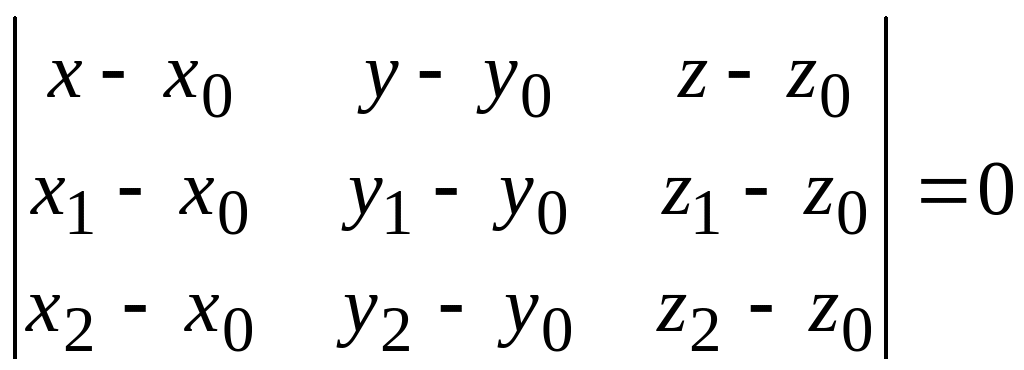 .
(6)
.
(6)
Если, в частности,
точки
являются
точками пересечения плоскости
с осями координат
![]() соответственно и плоскость
не проходит через начало координат
соответственно и плоскость
не проходит через начало координат
![]() ,
то эти точки имеют координаты:
,
то эти точки имеют координаты:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то уравнение (6) принимает вид:
,
то уравнение (6) принимает вид:
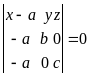 ,
,
или
![]() ,
и называется уравнением
плоскости
«в отрезках».
,
и называется уравнением
плоскости
«в отрезках».