
- •Глава 1. Метод координат в пространстве. Векторное и смешанное произведения векторов
- •§ 1. Аффинная система координат в пространстве.
- •§ 2. Прямоугольная декартова система координат в пространстве. Расстояние между двумя точками
- •§ 3. Ориентация пространства
- •§4. Формулы преобразования координат в
- •§ 5. Векторное произведение векторов и его свойства
- •§8. Смешанное произведение векторов
- •§ 7. Геометрическое истолкование уравнений и неравенств между координатами
§4. Формулы преобразования координат в
пространстве
1.Рассмотрим
в пространстве
две
аффинные
системы
координат
![]() и
и
![]() .
Первую
систему
назовем
"старой",
а
вторую
- "новой"
. Пусть
.
Первую
систему
назовем
"старой",
а
вторую
- "новой"
. Пусть
![]() - произвольная
точка
пространства
, которая
в старой
системе
координат
имеет
координаты
- произвольная
точка
пространства
, которая
в старой
системе
координат
имеет
координаты
![]() ,
,![]() ,
,
а в новой системе -
,
,
а в новой системе -
![]() :
:
![]() и
и
![]() .
.
Задача преобразования координат состоит в следующем: зная координаты "нового" начала координат и "новых" координатных векторов в "старой " системе:
|
|
![]()
![]() (
4)
(
4)
![]()
выразить (старые) координаты , , точки через (новые) координаты той же точки .
Так
как
![]() ,
(*)
,
(*)
то воспользовавшись формулами (1), (2), (3), (4) и сравнив одноименные координаты векторов, стоящих в левых частях равенства (* ), получим :
![]()
![]() (
5 )
(
5 )
![]()
Формулы (5) определяют искомую зависимость между старыми и новыми координатами точки и называются формулами преобразования аффинной системы координат в пространстве.
Заметим,
что в этих
формулах
коэффициенты
при
являются
соответственно
координатами новых
координатных
векторов
![]() относительно базиса
относительно базиса
![]() , и свободные члены
, и свободные члены
![]() - координатами нового
начала
- координатами нового
начала
![]() относительно
старой системы
координат
относительно
старой системы
координат
Заметим,
что в этих
формулах
матрица С =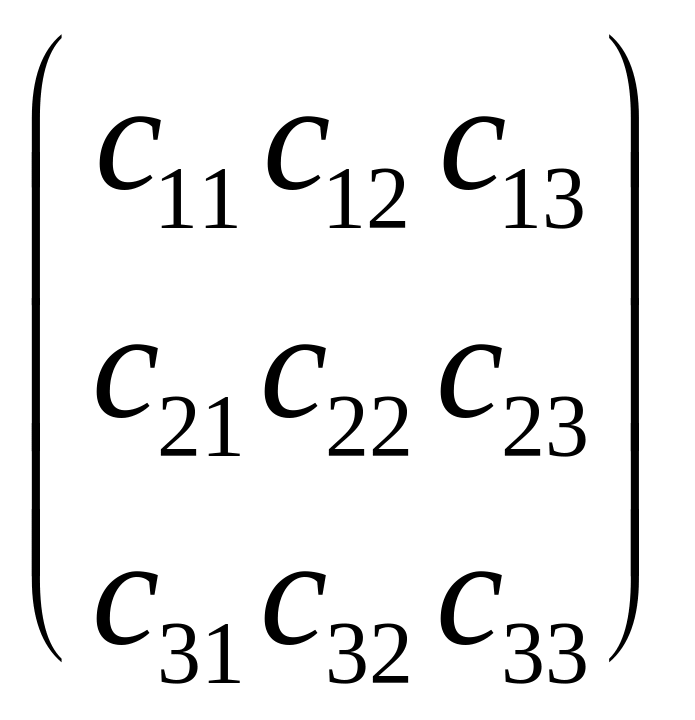 ,
составленная
из
коэффициентов при
,
есть
в точности матрица перехода от базиса
,
составленная
из
коэффициентов при
,
есть
в точности матрица перехода от базиса
![]() к базису
.
к базису
.
Так
как векторы
не
компланарны, то определитель матрицы
С не равен нулю, det(C)![]() 0.
Поэтому система (5) разрешима относительно
.
Это позволяет выразить координаты точки
в новой системе через координаты той
же точки в старой системе.
0.
Поэтому система (5) разрешима относительно
.
Это позволяет выразить координаты точки
в новой системе через координаты той
же точки в старой системе.
Если
в частности, новая система координат
![]() отличается от старой
лишь началом координат (перенос начала),
то формулы (5) принимают
вид:
отличается от старой
лишь началом координат (перенос начала),
то формулы (5) принимают
вид:
|
|
Если новая система координат отличается от старой лишь координатными векторами (замена координатных векторов), то формула (5) принимают вид :
![]()
![]() (7)
(7)
![]()
2.
Рассмотрим теперь преобразование
прямоугольных систем координат.В
случае
перехода
от одной
прямоугольной
системы
координат
![]() к
другой
к
другой
![]() получаем формулы преобразования
координат вида ( 5 ) , так как прямоугольная
система координат является частным
случаем аффинной . В данном случае на
элементы матрицы С накладываются
дополнительные ограничения: элементы
столбцов матрицы С являются соответственно
координатами единичных
и
взаимно
ортогональных
векторов
получаем формулы преобразования
координат вида ( 5 ) , так как прямоугольная
система координат является частным
случаем аффинной . В данном случае на
элементы матрицы С накладываются
дополнительные ограничения: элементы
столбцов матрицы С являются соответственно
координатами единичных
и
взаимно
ортогональных
векторов
![]() в ортонормированном
базисе
(
в ортонормированном
базисе
(![]() ),
поэтому
сумма
квадратов
элементов
каждого
столбца
матрицы
С равна
единице
, а сумма
произведений
соответствующих
элементов
любых двух
ее
различных
столбцов
равна
нулю.
),
поэтому
сумма
квадратов
элементов
каждого
столбца
матрицы
С равна
единице
, а сумма
произведений
соответствующих
элементов
любых двух
ее
различных
столбцов
равна
нулю.
По формулам § 2 получаем :



Отсюда,
учитывая эти соотношения, замечаем ,что
векторы
![]() в базисе (
)
имеют координаты :
в базисе (
)
имеют координаты :
![]()
![]()
![]()
Таким образом, сумма квадратов каждой строки матрицы С равна единице, а сумма произведений соответствующих элементов любых двух ее различных строк равна нулю .
Квадратная матрица С, обладающая такими свойствами, называется ортогональной.
Следовательно,
матрица
С
перехода
от
ортонормированного
базиса
(
![]() )
к ортонормированному
базису
(
)
является
ортогональной.
)
к ортонормированному
базису
(
)
является
ортогональной.
Матрица
С![]() ( обратная матрице
С
) перехода от базиса (
)
к базису (
)
совпадает с матрицей С
( обратная матрице
С
) перехода от базиса (
)
к базису (
)
совпадает с матрицей С![]() ,
транспонированной
к
матрице С, и, значит,
,
транспонированной
к
матрице С, и, значит,
det (С ) = det (С ) = det (С) .
Так
как det (С
)
=
![]() , то для ортогональной матрицы С
имеем:
, то для ортогональной матрицы С
имеем:
![]() ,
,
знак плюс имеет место в том случае, когда базисы ( ) и ( ) ориентированы одинаково , и знак минус, когда ориентированы противоположно.


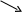






 (
6 )
(
6 )