Глава 1. Метод координат в пространстве. Векторное и смешанное произведения векторов
§ 1. Аффинная система координат в пространстве.
Деление отрезка в данном отношении
1.
Аффинным
репером
в пространстве называется упорядоченная
четверка точек пространства, не лежащих
в одной плоскости
:
=
(
,
).
Следовательно, никакие три из этих
точек не лежат на одной прямой.
Аффинный
репер
называют также общим
декартовым
репером
или аффинной
системой
координат
или общей
декартовой
системой
координат
в пространстве, а точку
- началом
репера
или началом
системы
координат.
Направленные
отрезки
(
=
1,2,3) определяют векторы
,
образующие базис (
,
,
)
трехмерного векторного пространства
.
Обратно задание точки
и какого-либо базиса (
,
,
)
векторного пространства
приводит к заданию аффинного репера
=
(
,
).,
где
- такие три точки, что
=
.
Следовательно, репер
можно задать точкой
и тремя некомпланарными векторами
(координатные
векторы);
поэтому пишут:
.
|
На
оси OAi
положительное
направление определяется вектором
.
Оси ( |
)=
,
(
)=(
),
(
)=
называются соответственно осями
абсцисс,
ординат
и апликат
(оси координат ).Плоскости
(
)=(
),
(
)=(
),
(
)=
=(
)
называются координатными
плоскостями
. На них заданы аффинные реперы:
=
(
)
на плоскости (
),
=(
,
)
на плоскости (
),
=
(
,
)
на плоскости (
).
Пусть
-
произвольная точка пространства. Вектор
( радиус - вектор точки
) можно разложить по вектором базиса
(
)
векторного пространства
,
и это разложение единственно ( теорема
о разложении вектора по векторам базиса
векторного пространства):
=
+ y
+ z
,
(
)
Координаты
радиус - вектора
точки
относительно базиса (
)
называются координатами
точки
относительно репера
=
(
),
- абсцисса
, у - ордината
,
z - апликата
(или первая , вторая, третья координаты)
точки
.
Пишут:
(
).
Итак,
(
)
=
+ y
+
,
(
).
Задание
аффинного репера
пространства устанавливает биективное
отображение ( взаимно однозначное
соответствие) множества точек
пространства на множество упорядоченных
троек их координат (
)
=
- декартов куб множества действительных
чисел.
Если
точка
имеет координаты
относительно репера
=
(
,
,
,
),
то
=
+ y
+
=
+
, где
=
+ y
,
=
,
(
)
//
(
)
,
если
.
Точка
называется проекцией
точки
на
плоскость
в
направлении
прямой
.
( , у) относительно репера = ( ) на плоскости ( у).
(
,у,
0 ) относительно репера
=
(
,
,
,
)
в пространстве .
Аналогично,
- проекция точки
на плоскость (
)
в направлении (
)
и
- проекция точки
на плоскость (
)
в направлении (
)
, то эти точки имеют координаты :
(y,
)
,
(0,y,
)
,
(
,
)
,
(
,0,z)
,
Рассмотрим
векторные проекции
,
,
вектора
|
= + + . |
=
на
оси координат (
),(
),
(
)
параллельно координатным плоскостям
(
),
(
),(
)
соответственно. Получим , что В
силу единственности разложения вектора
по трем некомпланарным векторам
,
,
, заключаем , что
являются координатами векторов
,
,
по векторам
,
,
соответственно, то есть скалярными
проекциями вектора
на оси координат.
Ломаную
называют
координатной
ломаной
точки
.
Ее используют при построении точки
по заданным координатам:
=
+
+
,
где
=
,
=
y
,
=
.
Если
апликата
точки
равна нулю, то
=
x
+ y
Векторы
,
,
линейно зависимы и поэтому они компланарны.
Это означает, что точка
лежит в плоскости (
)
и
(
)
.
Аналогично замечаем, что если
,
то точка
лежит в плоскости (
),
а если
,
то в плоскости (
).
Отсюда следует, что для любой точки
оси абцисс
,
для любой точки оси ординат
,
а для любой точки оси апликат
.
Начало координат имеет координаты
(0,0,0).
2.Рассмотрим две задачи, которые часто используются в курсе геометрии.
Задача1.В
аффинной
системе координат
=(
,
,
,
)
даны точки
и
.
Найти координаты вектора
.
Решение
.
Имеем :
=
-
,
так
как
+
=
( по правилу треугольника
сложения
векторов).
Но векторы
и
являются радиус -векторами точек
и
,
поэтому
.Таким
образом, вектор
имеет
координаты :
.
Итак, каждая координата вектора равна разности соответствующих координат конца и начала вектора .
Задача 2. В аффинной системе координат
=
(О,
,
,)
даны точки
и
Найти
координаты точки
,
которая делит отрезок
в отношении
, где
.
Решение.
(
,
)=
=
.
|
Откуда
имеем :
= |
.Тогда
x
=
,
у
=
,
z
=
В
частности , середина отрезка
имеет координаты (
)
:
x
=
,
у
=
,
z
=
.
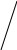
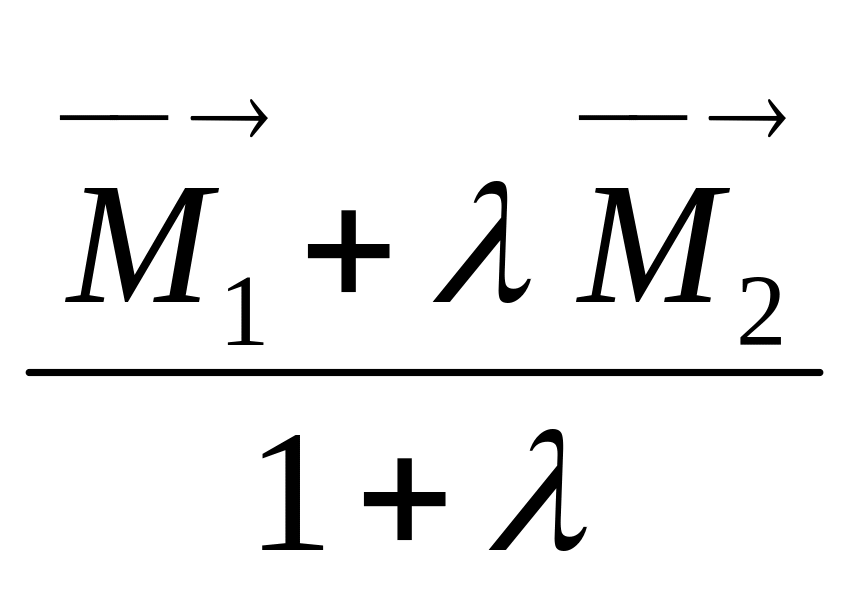