Нахождение линии тренда методом скользящей средней
Этот метод основан на последовательном вычислении набора средних значений из постоянного числа уровней ряда. Обычно это число выбирают нечетным от 3 и более.
Определение скользящих средних для рассматриваемого ряда динамики выглядит следующим образом:
Динамика объема продаж автомобилей
Номер |
Период |
Объем |
Скользящая |
Скользящая |
уровня |
|
продаж |
сумма |
средняя |
|
|
|
|
|
1 |
1985 |
3 |
- |
3,5 |
2 |
1986 |
4 |
11 |
3,7 |
3 |
1987 |
4 |
14 |
4,7 |
4 |
1988 |
6 |
17 |
5,7 |
5 |
1989 |
7 |
22 |
7,3 |
6 |
1990 |
9 |
26 |
8,7 |
7 |
1991 |
10 |
32 |
10,7 |
8 |
1992 |
13 |
38 |
12,7 |
9 |
1993 |
15 |
44 |
14,7 |
10 |
1994 |
16 |
52 |
17,3 |
11 |
1995 |
21 |
61 |
20,3 |
12 |
1996 |
24 |
73 |
24,3 |
13 |
1997 |
28 |
81 |
27,0 |
14 |
1998 |
29 |
- |
30,5 |
Выбор числа уровней для расчета средних основан на следующих соображениях:
Чем больше это число, тем выше эффект сглаживания. Однако при этом все более сокращается полученный ряд трендовых значений. При трехуровневых средних число этих значений уменьшилось на два по сравнению с исходным рядом.
Иногда прибегают к заполнению концов трендового ряда условными скользящими средними. Один из рекомендуемых способов предполагает их вычисление по следующим формулам:
Нахождение линии тренда методом аналитического выравнивания
Этот метод наиболее математически обоснован и, поэтому, чаще всего используется для выявления линии тренда.
Рассмотрим его на примере другого ряда динамики.
Динамика курса акций АО "Динамо"
Дата |
Условные |
Объем |
Квадраты |
Произведение |
Трендовые |
Квадраты |
|
|
моменты времени |
продаж |
моментов времени |
наблюдаемых значений |
времени на признак |
значения |
трендовых значений |
|
|
|
|
|
|
|
|
01.01.97 |
-4 |
8 |
16 |
64 |
– 32 |
7,3 |
53 |
01.04.97 |
-3 |
11 |
9 |
121 |
– 33 |
9,3 |
86 |
01.07.97 |
-2 |
12 |
4 |
144 |
– 24 |
11,3 |
127 |
01.10.97 |
-1 |
10 |
1 |
100 |
– 10 |
13,2 |
175 |
01.01.98 |
0 |
14 |
0 |
196 |
0 |
15,2 |
232 |
01.04.98 |
1 |
17 |
1 |
289 |
17 |
17,2 |
296 |
01.07.98 |
2 |
20 |
4 |
400 |
40 |
19,2 |
368 |
01.10.98 |
3 |
19 |
9 |
361 |
57 |
21,2 |
448 |
01.01.99 |
4 |
26 |
16 |
676 |
104 |
23,2 |
536 |
|
0 |
137 |
60 |
2351 |
119 |
137 |
2321 |
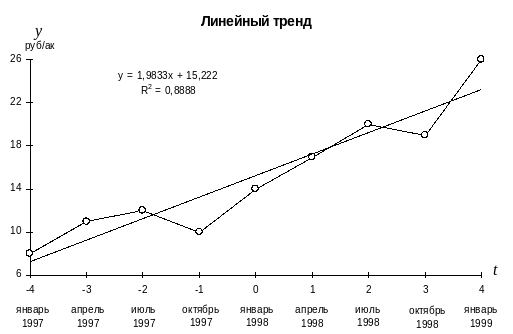
Если график ряда динамики условно рассматривать как аналог корреляционного поля, то можно сформулировать задачу нахождения такой линии, которая пройдет максимально близко одновременно ко всем имеющимся точкам. Математически эта задача решается с помощью метода наименьших квадратов.
Предварительно на основе визуального анализа расположения точек может быть выбран тип математической функции, с помощью которой будет описана линия тренда.
Предположим, что эта функция соответствует уравнению прямой линии:
,
где
– трендовые значения уровней ряда динамики,
и
– искомые параметры линии тренда,
– характеристика
времени.
Применяя метод наименьших квадратов к этой функции можно получить систему нормальных уравнений, позволяющую вычислить значения искомых параметров. Для прямой линии имеем:
,
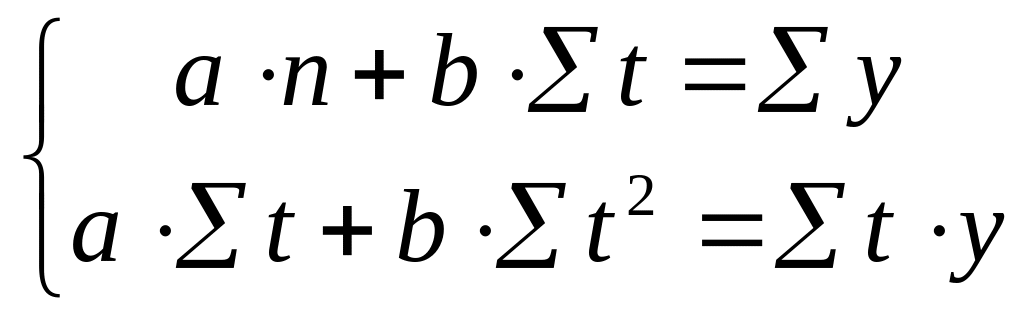где
– число уровней ряда динамики.
В принципе эта система позволяет устанавливать параметры линии тренда. Вместе с тем, для подстановки в нее характеристики времени ( ) необходимо уточнить ее числовое представление.
Исчисление времени всегда требует применения определенной шкалы, в которой установлена точка отсчета. Так, например, 1999 – это порядковый номер года от Рождества Христова. Можно считать точкой отсчета времени начало текущего века. Тогда тот же год будет количественно представлен числом 99.
Еще один вариант точки отсчета времени может быть принят соответствующим первому уровню исследуемого ряда динамики. Для рядов с интервалом менее года такой подход разумен. Иначе пришлось бы считать число кварталов или месяцев от Рождества Христова или от начала века.
Поскольку при анализе конкретного ряда динамики точку отсчета времени можно выбирать произвольно, то представляется целесообразным ее выбрать так, чтобы расчет параметров линии тренда был бы наиболее простым. Из этих соображений для конкретного ряда динамики можно построить индивидуальную шкалу времени, отвечающую двум условиям:
Во-первых, числовые расстояния между двумя соседними значениями должны быть одинаковыми. Это обеспечивает соблюдение масштаба измерения времени, так как продолжительность периодов между двумя уровнями как правило равновелика. Так, в рассматриваемом ряду такая продолжительность соответствует кварталу.
Во-вторых, сумма всех значений , имеющихся в данном ряду, должна быть равна нулю. Очевидно данное условие будет выполняться, когда точка отсчета времени будет строго совпадать с центром исследуемого ряда динамики.
Способ решения этой задачи зависит от числа уровней анализируемого ряда динамики. Если число уровней нечетно, то точка отсчета времени будет соответствовать тому уровню, который занимает центральное положение в ряду. Порядковый номер этого уровня можно определить как
.
Для центрального уровня значение временной характеристики принимается равным нулю. У остальных уровней значение времени принимается с шагом равным 1, для предшествующих уровней – со знаком минус, для последующих – со знаком плюс.
Если, например, ряд динамики насчитывает 9 уровней, то для него целесообразно использовать следующую временную шкалу:
Условная характеристика времени |
|
Порядковый номер уровня |
1 2 3 4 5 6 7 8 9 |
Легко убедиться, что для построенной таким образом временной шкалы выполняются оба наложенных условия. Числовое расстояние между двумя соседними значениями везде одинаково и равно единице, а сумма всех значений равна нулю.
Если число уровней ряда четно, то точка отсчете времени должна быть выбрана посередине между двумя уровнями, образующими сдвоенный центр ряда. Порядковые номера этих уровней определяются как:
,
Левому уровню центра можно присвоить значение времени, равное –1, а правому – +1.
У остальных уровней временная характеристика будет устанавливаться с шагом равным 2, для предшествующих уровней – со знаком минус, для последующих – со знаком плюс.
Если, например, ряд динамики насчитывает 10 уровней, то для него целесообразно использовать следующую временную шкалу:
Условная характеристика времени |
|
Порядковый номер уровня |
1 2 3 4 5 6 7 8 9 10 |
В этой шкале также выполняются оба наложенных условия. Числовое расстояние между двумя соседними значениями везде одинаково и равно двум, а сумма всех значений равна нулю.
Для ряда с четным числом уровней можно построить и другую временную шкалу (с дробными значениями):
Условная характеристика времени |
|
Порядковый номер уровня |
1 2 3 4 5 6 7 8 9 10 |
Однако практическое использование такой шкалы оказывается менее удобным.
Поскольку в рассматриваемом ряде динамики число уровней нечетно, то для количественного представления времени можно использовать соответствующую временную шкалу, из которой значения условных моментов времени показываются во второй графе расчетной таблицы.
После преобразования характеристики времени вернемся снова к системе нормальных уравнений.
Поскольку
,
то можно записать:
Отсюда легко выводятся формулы для непосредственного вычисления параметров прямой линии тренда:
,
Вычислим эти параметры для рассматриваемого примера на основе вспомогательных расчетов в соответствующих колонках таблицы.
,
Следовательно, уравнение линии выглядит следующим образом:
В соответствии с этим уравнением для каждого уровня ряда можно рассчитать трендовое значение. Сумма всех трендовых значений должна совпадать с суммой зарегистрированных (эмпирических) значений.
При подборе математической функции для описания линии тренда возникает вопрос о том, насколько удачно сделан выбор. Степень такой удачности отражается через близость наблюдаемых и трендовых значений. По аналогии с корреляционно-регрессионным анализом в качестве количественной меры этой близости можно принять коэффициент детерминации, определяемый соотношением объясненной и общей дисперсии исследуемого признака. Очевидно, общая дисперсия должна рассчитываться из набора наблюдаемых, а объясненная – из набора трендовых значений.
Используя результаты вспомогательных расчетов в таблице определим соответствующие показатели:
– общая
дисперсия
– объясненная
дисперсия
– коэффициент
детерминации
Поскольку полученное значение коэффициента детерминации достаточно близко к 1, то можно утверждать, что прямолинейный тренд довольно хорошо описывает долговременную тенденцию.
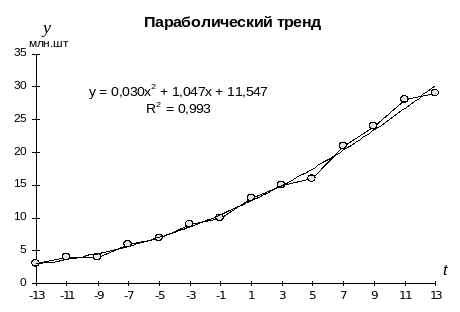
В качестве эксперимента для описания линии тренда можно подобрать несколько других математических функций.
Сравнивая
значения коэффициентов детерминации
при различных вариантах линии тренда
можно установить, что наиболее точно
описывает долговременную тенденцию
параболический тренд. Вместе с тем,
степень его достоверности не на много
отличается от линейного тренда (
).
Поскольку прямая линия дает более
простое описание динамического процесса,
то для окончательного представления
долговременной тенденции целесообразно
принять линейный тренд в виде функции
.
Для дальнейшего анализа ряда динамики необходимо исключить установленный тренд, что позволяет перейти к так называемому стационарному ряду.
.
Разложение ряда динамики на компоненты
Момент времени |
Значение времени |
Объем продаж |
Трендовые значения |
Отклонения от тренда |
Сезонная компонента |
Случайная компонента |
Расчет частных дисперсий |
||
|
|
|
|
|
|
|
|
|
|
01.01.97 |
-4 |
8 |
7,3 |
0,7 |
0,78 |
-0,1 |
0,506 |
0,605 |
0,004 |
01.04.97 |
-3 |
11 |
9,3 |
1,7 |
0,76 |
1,0 |
2,985 |
0,579 |
0,934 |
01.07.97 |
-2 |
12 |
11,3 |
0,7 |
0,78 |
0,0 |
0,554 |
0,605 |
0,001 |
01.10.97 |
-1 |
10 |
13,2 |
-3,2 |
-2,71 |
-0,5 |
10,490 |
7,320 |
0,284 |
01.01.98 |
0 |
14 |
15,2 |
-1,2 |
0,78 |
-2,0 |
1,494 |
0,605 |
4,000 |
01.04.98 |
1 |
17 |
17,2 |
-0,2 |
0,76 |
-1,0 |
0,042 |
0,579 |
0,934 |
01.07.98 |
2 |
20 |
19,2 |
0,8 |
0,78 |
0,0 |
0,658 |
0,605 |
0,001 |
01.10.98 |
3 |
19 |
21,2 |
-2,2 |
-2,71 |
0,5 |
4,719 |
7,320 |
0,284 |
01.01.99 |
4 |
26 |
23,2 |
2,8 |
0,78 |
2,1 |
8,091 |
0,605 |
4,271 |
|
0 |
137 |
137 |
0 |
0 |
0 |
29,54 |
18,82 |
10,72 |
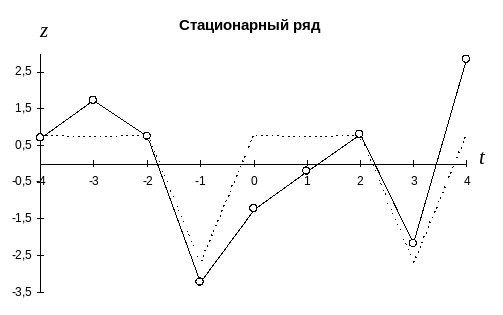
Для выделения в стационарном ряду сезонной компоненты также можно использовать различные методы, к основными из которых являются:
– расчет индексов сезонности,
– гармонический анализ.
Расчет индексов сезонности
Основан на аналитической группировке отклонений от тренда по однотипным моментам или периодам внутри года. Для определения индексов сезонности можно использовать следующее выражение:
,
где
– число
уровней ряда динамики, относящихся к
соответствующему сезону.
Расчет индексов сезонности
-
1997
1998
1999
Сумма остатков
Индексы сезонности
1 января
0,7
-1,2
2,8
2,3
0,7778
1 апреля
1,7
-0,2
1,5
0,7611
1 июля
0,7
0,8
1,6
0,7778
1 октября
-3,2
-2,2
-5,4
-2,706
-0,1
-2,8
2,8
0,0
После исключения из стационарного ряда сезонной компоненты можно получить набор значений остатков, который описывает поведение случайной компоненты.
О значимости каждой из трех выделенных компонент с точки зрения их влияния на интенсивность динамического процесса можно судить по величине соответствующих дисперсий.
– дисперсия
отклонений от тренда
– дисперсия
сезонных колебаний
– дисперсия
случайных колебаний
Полную схему разложения общей дисперсии исследуемого признака целесообразно свести в специальную таблицу.
Дисперсия |
|
общая |
29,506 |
тренда |
26,224 |
остатков |
3,282 |
сезонная |
2,091 |
случайная |
1,191 |
Гармонический анализ
При использовании гармонического анализа предполагается, что сезонная волна может быть описана с помощью периодической функции вида:
.
Поскольку производный ряд отклонений от тренда является стационарным, то свободный член этого уравнения оказывается равным нулю.
.
Применяя к этому выражению метод наименьших квадратов можно получить прямые формулы для вычисления параметров:
,
Расчет параметров функции сезонной волны
Момент времени |
|
|
|
|
|
|
|
|
|
|
|
01.01.97 |
-4 |
8 |
7,3 |
0,7 |
0 |
1 |
0 |
0,71 |
0,00 |
0,17 |
0,54 |
01.04.97 |
-3 |
11 |
9,3 |
1,7 |
90 |
0 |
1 |
0,00 |
1,73 |
1,54 |
0,19 |
01.07.97 |
-2 |
12 |
11,3 |
0,7 |
180 |
-1 |
0 |
-0,74 |
0,00 |
-0,17 |
0,92 |
01.10.97 |
-1 |
10 |
13,2 |
-3,2 |
270 |
0 |
-1 |
0,00 |
3,24 |
-1,54 |
-1,70 |
01.01.98 |
0 |
14 |
15,2 |
-1,2 |
0 |
1 |
0 |
-1,22 |
0,00 |
0,17 |
-1,40 |
01.04.98 |
1 |
17 |
17,2 |
-0,2 |
90 |
0 |
1 |
0,00 |
-0,21 |
1,54 |
-1,75 |
01.07.98 |
2 |
20 |
19,2 |
0,8 |
180 |
-1 |
0 |
-0,81 |
0,00 |
-0,17 |
0,98 |
01.10.98 |
3 |
19 |
21,2 |
-2,2 |
270 |
0 |
-1 |
0,00 |
2,17 |
-1,54 |
-0,63 |
01.01.99 |
4 |
26 |
23,2 |
2,8 |
0 |
1 |
0 |
2,84 |
0,00 |
0,17 |
2,67 |
|
0 |
137 |
137 |
0 |
– |
– |
– |
0,78 |
6,93 |
0,17 |
-0,17 |
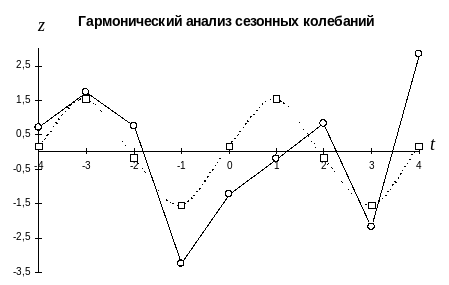
Для рассматриваемого примера параметры гармонической функции сезонных колебаний определяются следующими равенствами:
,
.
Следовательно, сезонная волна может быть описана уравнением
.
По аналогии с представлением сезонной компоненты через индексы сезонности здесь можно показать разложение общей дисперсии на отдельные составляющие.
Дисперсия |
|
общая |
29,506 |
тренда |
26,224 |
остатков |
3,282 |
сезонная |
1,071 |
случайная |
1,950 |
Нахождение линии тренда методом аналитического выравнивания
Динамика объема продаж автомобилей
|
Значение |
Объем |
Трендовые |
Период |
времени |
продаж |
значения |
|
|
|
|
1985 |
-13 |
3 |
-0,1 |
1986 |
-11 |
4 |
2,0 |
1987 |
-9 |
4 |
4,1 |
1988 |
-7 |
6 |
6,2 |
1989 |
-5 |
7 |
8,3 |
1990 |
-3 |
9 |
10,4 |
1991 |
-1 |
10 |
12,5 |
1992 |
1 |
13 |
14,5 |
1993 |
3 |
15 |
16,6 |
1994 |
5 |
16 |
18,7 |
1995 |
7 |
21 |
20,8 |
1996 |
9 |
24 |
22,9 |
1997 |
11 |
28 |
25,0 |
1998 |
13 |
29 |
27,1 |
|
0 |
189 |
189 |
Динамика объема продаж автомобилей
|
Значение |
Объем |
Трендовые |
Период |
времени |
продаж |
значения |
|
|
|
|
1985 |
-13 |
3 |
3,3 |
1986 |
-11 |
4 |
4,0 |
1987 |
-9 |
4 |
4,7 |
1988 |
-7 |
6 |
5,7 |
1989 |
-5 |
7 |
6,8 |
1990 |
-3 |
9 |
8,1 |
1991 |
-1 |
10 |
9,7 |
1992 |
1 |
13 |
11,6 |
1993 |
3 |
15 |
13,9 |
1994 |
5 |
16 |
16,6 |
1995 |
7 |
21 |
19,9 |
1996 |
9 |
24 |
23,8 |
1997 |
11 |
28 |
28,5 |
1998 |
13 |
29 |
34,1 |
|
0 |
189 |
191 |
Динамика объема продаж автомобилей
|
Значение |
Объем |
Трендовые |
Период |
времени |
продаж |
значения |
|
|
|
|
1985 |
-13 |
3 |
3,0 |
1986 |
-11 |
4 |
3,7 |
1987 |
-9 |
4 |
4,6 |
1988 |
-7 |
6 |
5,7 |
1989 |
-5 |
7 |
7,1 |
1990 |
-3 |
9 |
8,7 |
1991 |
-1 |
10 |
10,5 |
1992 |
1 |
13 |
12,6 |
1993 |
3 |
15 |
15,0 |
1994 |
5 |
16 |
17,5 |
1995 |
7 |
21 |
20,4 |
1996 |
9 |
24 |
23,4 |
1997 |
11 |
28 |
26,7 |
1998 |
13 |
29 |
30,2 |
|
0 |
189 |
189 |
