Анализ рядов динамики
Более детальную информацию о ряде динамики можно получить с помощью его разложения на отдельные составляющие (компоненты). В общем случае к их числу относятся:
– долговременная тенденция (тренд) – T
– многолетние циклические колебания – C
– сезонные колебания – S
– случайные колебания – A
Долговременная тенденция отражает общую закономерность развития изучаемого явления. Она рассматривается как долгосрочная компонента, действующая с определенной устойчивостью на протяжении всего периода времени, для которого построен ряд.
Многолетние циклические колебания образуются под воздействием особых причин, действующих волнообразно с периодичностью в несколько лет. Обычно эта компонента связывается с периодами деловой активности в развитом рыночном хозяйстве, с инвестиционными или строительными циклами. Практически во всех статистических исследования, проводимых в нашей стране, эта составляющая пока не рассматривается, поскольку основания для нее еще не сформировались.
Сезонные колебания возникают за счет изменения погодных условий, различий в характере производства и потребления некоторых продуктов в отдельные времена года. Особенностью этой компоненты является регулярная повторяемость во времени с периодичность, равной году. Выделить сезонные колебания удается для рядов, интервалы которых оказываются менее года (дневные, месячные, квартальные). Если ряд имеет интервалы от года и более, то сезонная компонента остается скрытой внутри каждого отдельного уровня, что не позволяет ее выявить и описать.
Случайные колебания связаны с воздействием на изучаемое явление множества различных причин, влияние которых имеет разовый или не регулярный характер.
Для проведения анализа ряда динамики все присущие для него компоненты должны быть объединены в общую модель. Различают два типа подобных моделей:
1. Мультипликативная, в которой любой уровень ряда динамики образуется в виде произведения отдельных компонент.
(многолетние
циклические колебания в этой модели не
выделены и объединены со случайной
компонентой).
2. Аддитивная, в которой уровни ряда формируются как сумма отдельных компонент.
При использовании в анализе аддитивной модели предполагается, что воздействие на уровни сезонной компоненты имеет неизменный характер на протяжении всего периода динамики. Другими словами, интенсивность сезонных колебаний сохраняется одинаковой из года в год.
В мультипликативной модели предполагается, что с течением времени амплитуда сезонных колебаний может изменяться. Так, при положительном тренде эта амплитуда будет возрастать.
В большинстве исследований подобные особенность во внимание не принимаются и отдается предпочтение аддитивной модели, как наиболее простой с точки зрения аналитических расчетов.
Итак, будем считать, что анализ проводится с помощью аддитивной модели вида:
– для рядов с периодом меньше года
или
– для
рядов с периодом от года и более.
Анализ всегда начинается с выявления и описания долговременной тенденции (тренда).
Методы выявления долговременной тенденции
В статистике разработаны различные методы выявления и описания линии тренда.
К наиболее распространенным из них относятся:
– метод средних значений,
– с помощью средних абсолютных приростов,
– с помощью средних темпов роста,
– метод скользящей средней,
– метод аналитического выравнивания.
Заметим, что основная идея любого из этих методов заключается в сглаживании (выравнивании) колебаний уровней ряда.
Нахождение линии тренда методом средних значений
Метод средних значений предполагает разделение ряда на две равные части с последующим вычислением в каждой из них своего среднего уровня.
Динамика объема продаж автомобилей
Номер |
Период |
Объем |
Средние |
уровня |
|
продаж |
уровни |
|
|
|
|
1 |
1985 |
3 |
-0,06122 |
2 |
1986 |
4 |
2,102041 |
3 |
1987 |
4 |
4,265306 |
4 |
1988 |
6 |
6,1 |
5 |
1989 |
7 |
8,591837 |
6 |
1990 |
9 |
10,7551 |
7 |
1991 |
10 |
12,91837 |
8 |
1992 |
13 |
15,08163 |
9 |
1993 |
15 |
17,2449 |
10 |
1994 |
16 |
19,40816 |
11 |
1995 |
21 |
20,9 |
12 |
1996 |
24 |
23,73469 |
13 |
1997 |
28 |
25,89796 |
14 |
1998 |
29 |
28,06122 |
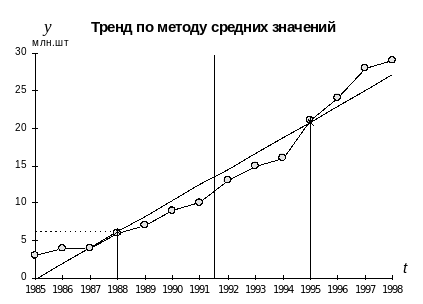
Поскольку средние уровни рассчитываются для интервального ряда, то следует воспользоваться средней арифметической (простой).
