
- •1. Понятия теоретической механики: материальная точка, твердое тело, равнодействующая сила
- •2. Определения и понятия механики: система сил, эквивалентная сила, равнодействующая сила
- •3. Понятия: Связь тела, опора, виды типовых опор
- •4. Проекция сил на оси координат, разложение силы по ортогональным осям на составляющие
- •5. Условия равновесия плоской системы сходящихся сил, система уравнений равновесия
- •6. Равнодействующая плоской системы параллельных сил, расчет координаты приложения равнодействующей
- •7. Параллельный перенос сил на плоскости (теорема Пуансо)
- •12. Состав рабочей машины: звено, узел, механизм, привод
- •13.Структурный анализ механизмов, термины и понятия: звено, кинематическая цепь
- •14. Понятие степень свободы, число степеней свободы плоских и пространственных механизмов, подвижность механизмов
- •15. Структурный анализ плоского рычажного механизма, оценка его подвижности
- •16 . Структурный анализ пространственного рычажного механизма, оценка его подвижности
- •17. Схемы плоских шарнирно-стержневых механизмов, термины: кривошип, шатун, ползун, кулиса, коромысло.
- •17. Продолжение
- •17. Продолжение продолжения
- •18. Понятие «Кинематическая пара», виды кинематических пар, их условное графическое изображение
- •19. Кинематический анализ механизмов, суть и задачи анализа, термины: входное звено, закон движения, входная координата, передаточная функция
- •19. Продолжение
- •20. Кинематические характеристики механизмов: передаточное отношение, передаточное число. Определения, обозначения, свойства
- •23. Продолжение
- •24. Трение скольжения, сила трения, её свойства, условие равновесия т.Т на наклонной поверхности
- •25. Трение качения, условие равновесия при равномерном перекатывании, коэффициент трения качения, его свойства
- •27. Сила тяжести, центр тяжести, методы определения центра тяжести
- •28. Схемы плоских кулачковых механизмов, термины, оценка подвижности
- •28. Продолжение
- •28. Продолжение продолжения
- •29. Кинематические характеристики механизмов, передаточное число и отношение, свойства
- •4.Допущения, принимаемые при оценке свойств материала элементов при оценке прочности элементов конструкций
- •5.Принципы построения расчетных схем при оценке прочности. Гипотезы начальных размеров, независимости действия сил, плоских сечений
- •6. Виды составляющих внутренних сил в элементах конструкций, обозначение, классификация, виды нагружения
- •7. Оценка внутренних сил, метод сечения
- •8. Характеристики механических свойств материала, испытания материалов, диаграмма условных напряжений
- •9. Геометрические хар-ки плоских сечений элементов
- •9. Продолжение
- •11. Абсолютные и относительные перемещения элементов конструкции, деформация, виды деформации
- •12. Допускаемые напряжения, их расчет
- •13. Расчет на прочность при «растяжении-сжатии», внутренние силы, расчет напряжений, условие прочности
- •14. Расчет перемещений при «растяжении-сжатии», деформация, закон Гука.
- •15. Виды расчетов на прочность при «растяжении-сжатии»: проектный, проверочный, расчет допускаемой нагрузки.
- •16. Вид нагружения сдвиг, расчеты напряжений и перемещений при сдвиге
- •17. Вид нагружения 'кручение'. Расчет на прочность при кручении
- •17. Перемещения при кручении,их оценка.Расчет валов на жесткость
- •19. Вид нагружения «изгиб» внутренние силы, напряжения, их оценка
- •20. Схема расчета на прочность при изгибе, условия прочности при изгибе
- •21. Перемещения при изгибе, их расчет
- •22. Расчет на прочность при действии переменных напряжений, кривая усталости, предел выносливости
- •23. Проверочный расчёт по предельно допускаемым значениям напряжения:
- •24. Расчет на прочность при действии переменных напряжений, усталость, выносливость, кривая усталости, предел выносливости
- •25. Циклы переменных напряжений,параметры цикла
- •26. Параметры циклов пременных напряжений симметричного и отнулевого циклов.
- •27. Концентрация напряжений, оценка концентрации напряжений по теоретическому коэффициенту концентрации
- •28. Распределение напряжений в плоскости поперечных сечений при кручении и изгибе, рациональные формы поперечных сечений
- •29. Схема двухопорной балки при нагружении плоской системой произвольно расположенных сил, уравнения равновесия, расчёт реакции опоры
- •30. Кинематическая характеристики механизмов: передаточное число и передаточное отношение, их свойства
12. Состав рабочей машины: звено, узел, механизм, привод
Звено – твердое тело (деталь), одно или несколько неподвижно соединенных тел. Узел – часть машины, имеющая общее назначение среди других машин (прим. Шпиндельный узел). Механизм – часть машины, предназначенная для преобразования движения в машине. Привод – средство для передачи мощности от двигателя на рабочий орган.
13.Структурный анализ механизмов, термины и понятия: звено, кинематическая цепь
Структурный
анализ механизма позволяет установить
последовательность и методы его
кинематического и силового анализа,
поскольку стр-ные группы каждого класса
и вида обладают единством методов их
иссл-ния. Для струк. анализа механизмов
с высшими парами используется метод
построения заменяющих механизмов.
Сопоставим 2 механизма: 1-ый
с высшей парой, а 2-ой
заменяющий (без высших пар), причем оба
имеют одно и то же число степеней свободы
, т. е. откуда
откуда Если
Если
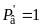 ,
то
,
то
 и
и
 .
Таким образом, одна высшая пара
эквивалентна одному добавочному звену,
входящему в две низшие пары.Одно или
несколько жестко соединенных твердых
тел, входящих в состав механизма,
называется звеном.В каждом механизме
имеется стойка, т. е. звено неподвижное
или принимаемое за неподвижное. Входным
звеном называется звено, которому
сообщается движение, преобразуемое
механизмом в требуемыедви-жения других
звеньев. Выходным-звено, совершающее
движение, для выполнения которого
предназначен механизм.Свободное тело
(звено) в пространстве обладает 6 степенями
свободы, так как оно может совершать 3
независимых поступательных движения
вдоль взаимно перпендикулярных
координатных осей и 3 вращательных
движения вокруг тех же осей. После того
как звено соединяется с другим звеном
посредством кин. пары, на его относительное
движение накладываются некоторые
ограничения (связи), причем № класса
кинематической пары определяется числом
наложенных связей. Кинематической цепью
называется система звеньев, связанных
между собой кинематическими парами.
К
.
Таким образом, одна высшая пара
эквивалентна одному добавочному звену,
входящему в две низшие пары.Одно или
несколько жестко соединенных твердых
тел, входящих в состав механизма,
называется звеном.В каждом механизме
имеется стойка, т. е. звено неподвижное
или принимаемое за неподвижное. Входным
звеном называется звено, которому
сообщается движение, преобразуемое
механизмом в требуемыедви-жения других
звеньев. Выходным-звено, совершающее
движение, для выполнения которого
предназначен механизм.Свободное тело
(звено) в пространстве обладает 6 степенями
свободы, так как оно может совершать 3
независимых поступательных движения
вдоль взаимно перпендикулярных
координатных осей и 3 вращательных
движения вокруг тех же осей. После того
как звено соединяется с другим звеном
посредством кин. пары, на его относительное
движение накладываются некоторые
ограничения (связи), причем № класса
кинематической пары определяется числом
наложенных связей. Кинематической цепью
называется система звеньев, связанных
между собой кинематическими парами.
К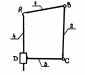
 ин.
цепи могут быть плоскими и пространственными,
замкнутыми и незамкнутыми. В плоской
цепи при закреплении одного из звеньев
все остальные совершают плоское движение,
параллельное одной и той же неподвижной
плоскости (рис. 5.1). В остальных случаях
кинематическая цепь является
пространственной (рис. 5.2). В замкнутой
кинематической цепи (см. рис. 5.1) звенья
образуют один или несколько замкнутых
контуров, а в незамкнутой цепи (см. рис.
5.2) звенья не образуют замкнутых контуров.
ин.
цепи могут быть плоскими и пространственными,
замкнутыми и незамкнутыми. В плоской
цепи при закреплении одного из звеньев
все остальные совершают плоское движение,
параллельное одной и той же неподвижной
плоскости (рис. 5.1). В остальных случаях
кинематическая цепь является
пространственной (рис. 5.2). В замкнутой
кинематической цепи (см. рис. 5.1) звенья
образуют один или несколько замкнутых
контуров, а в незамкнутой цепи (см. рис.
5.2) звенья не образуют замкнутых контуров.
Рис. 5.1. Замкнутая плоская цепь Рис. 5.2. Пространственная незамкнутая цепь
Кинематическая цепь входит в состав каждого механизма, образованного только из твердых тел.
14. Понятие степень свободы, число степеней свободы плоских и пространственных механизмов, подвижность механизмов
Степени свободы — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Также число степеней свободы равно полному числу независимых уравнений, полностью описывающих динамику системы. Под числом степеней подвижности механизма (обозначение W) будем понимать число независимых параметров, определяющих положение всех подвижных звеньев механизма.
Такими параметрами являются независимые координаты, определяющие положения входных звеньев. Очевидно, число степеней подвижности будет равно числу всех входных звеньев.
Для пространственных механизмов в настоящее время наиболее распространена формула Малышева, вывод которой производится следующим образом. Введём обозначения следующих числовых величин:
m –
число звеньев (включая стойку); p1, p2,
p3, p4, p5 – число одно-, двух-, трёх-,
четырёх - и пятиподвижных пар; n=m-1 –
число подвижных звеньев механизма. Если
бы все подвижные звенья были свободными
телами, общее число степеней свободы
было бы равно 6n. Однако каждая
одноподвижная пара V-го класса, накладывает
на относительное движение звеньев,
образующих пару 5 связей, каждая
двухподвижная пара IV-го класса – 4 связи
и т. д. Следовательно, общее число степеней
свободы, равное шести, будет уменьшено
на величину: рк=5р1+4р2+3р3+2р4+р5 . Пусть в плоском
механизме, имеющем m звеньев
(включая стойку), n=m-1 – число
подвижных звеньев, pн – число
низших пар и pв – число высших пар.
Если бы все подвижные звенья были
свободными телами, совершающими плоское
движение, общее число степеней свободы
было бы равно 3n. Однако каждая низшая
пара накладывает на относительное
движение звеньев, образующих пару, две
связи, а каждая высшая пара накладывает
одну связь, оставляя 2 степени свободы.
В число наложенных связей может войти
некоторое число qп избыточных
(повторных) связей, устранение которых
не увеличивает подвижности механизма.
Следовательно, число степеней свободы
плоского механизма, т.е. число степеней
свободы его подвижной кинематической
цепи, относительно стойки, определяется
по следующей формуле Чебышева:
рк=5р1+4р2+3р3+2р4+р5 . Пусть в плоском
механизме, имеющем m звеньев
(включая стойку), n=m-1 – число
подвижных звеньев, pн – число
низших пар и pв – число высших пар.
Если бы все подвижные звенья были
свободными телами, совершающими плоское
движение, общее число степеней свободы
было бы равно 3n. Однако каждая низшая
пара накладывает на относительное
движение звеньев, образующих пару, две
связи, а каждая высшая пара накладывает
одну связь, оставляя 2 степени свободы.
В число наложенных связей может войти
некоторое число qп избыточных
(повторных) связей, устранение которых
не увеличивает подвижности механизма.
Следовательно, число степеней свободы
плоского механизма, т.е. число степеней
свободы его подвижной кинематической
цепи, относительно стойки, определяется
по следующей формуле Чебышева:![]() Индекс “П” напоминает о том, что речь
идёт об идеально плоском механизме,
или, точнее, о его плоской схеме, поскольку
за счёт неточностей изготовления плоский
механизм в какой-то мере является
пространственным. Подвижность
механизма -
число независимых обобщенных координат
однозначно определяющих положение
звеньев механизма в пространстве.
Индекс “П” напоминает о том, что речь
идёт об идеально плоском механизме,
или, точнее, о его плоской схеме, поскольку
за счёт неточностей изготовления плоский
механизм в какой-то мере является
пространственным. Подвижность
механизма -
число независимых обобщенных координат
однозначно определяющих положение
звеньев механизма в пространстве.
