17. Перемещения при кручении,их оценка.Расчет валов на жесткость

С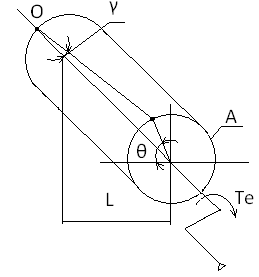 хема оценки деформации при кручении:

θ=TL/σI_ρ σ=8∙10⁴ МПа – модуль упругости второго рода

θ, γ,град I_ρ – полярный момент инерции

Для круглого сечения I_ρ=πd⁴/32

γ= =

Расчет на жесткость при кручении:

Проверяются след. условия γ_max≤ [γ] - 10℅

+ 5℅

В случае невыполнения данного усл. прводится проектный расчет

γ= =[γ], I_ρ=πd⁴/32 значит d_γ=

τ_max≤ [τ] γ_max≤ [γ] Из двух усл. выбирается d вала,удовл. обоим усл. d_τ d_γ

19. Вид нагружения «изгиб» внутренние силы, напряжения, их оценка

Изгиб – вид нагружения, при котором в поперечных сечениях элемента возникают изгибающие моменты М_х , М_{у ,} действующие в сечениях, перпендикулярных поперечному сечению элементов. Рассмотрим прямолинейный призматический брус с продольной плоскостью симметрии. Изгиб бруса силами, перпендикулярными его оси и лежащими в той же плоскости, через которую проходит ось бура, называется поперечным изгибом. Такой изгиб, когда в плоскости действия внешних нагрузок происходит деформация, называется плоским изгибом. Изгиб бруса, который происходит под действием двух равных моментов, направленных в противоположные стороны, называется чистым изгибом. Косой – плоскости действия изгибающей поверхности не совпадают с осями.

Элементы реальных конструкций часто испытывают деформацию изгиба, поэтому объектом решения во многих задачах являются балки или балочные системы.

В общем случае прямого изгиба в поперечных сечениях бруса возникают два внутренних силовых фактора:

1) поперечная сила( в любом поперечном сечении бруса численно равна алгебраической сумме проекций на ось У всех внешних сил, действующих по одну сторону от сечения)

2) изгибающий момент(равен сумме моментов, вычисленных относительно центра тяжести сечения, всех внешних сил, действующих по одну сторону от сечения)

При плоском изгибе в поперечном сечении возникают нормальные(σ) и касательные(τ) напряжения.

20. Схема расчета на прочность при изгибе, условия прочности при изгибе

КАК В КНИГЕ

Нормальные напряжения в поперечном сечении балки при изгибе: σ = (M_x/ J_x)Y_max , H/м²

где M_x – изгибающий момент в сечении балки, Н*м; Y_max - расстояние от нейтральной оси до рассматриваемого слоя волокон, м; J_x - осевой момент балки, м⁴.

Наибольшие нормальные напряжения при изгибе балки с сечением, симметричным относительно центральной оси: σ_max=M_xmax/W_x, Н/ м², где W_x - осевой момент сопротивления сечения балки, м³.

Прочность балки, работающей на изгиб, проверяется по наибольшим нормальным напряжениям: σ_max=M_xmax/W_x≤[σ], где [σ] – допускаемое напряжение при изгибе, МПа.

Касательные напряжения при изгибе балки определяются по формуле: τ = (QS)/(bJ_x), H/м², где Q – поперечная сила в сечении балки, Н; S - статический момент относительно нейтральной оси, м³ ; b – ширина рассматриваемого продольного слоя, м; J_x – осевой момент инерции, м⁴.

Условие прочности при изгибе балки по касательным напряжениям: τ _max=(Q _max S)/(bJ_x) ≤[τ]_, H/м², где [τ] – допускаемое касательное напряжение.

КАК В КОНСПЕКТЕ ТИЛИГУЗОВА

τ = (QS)/(bJ_x), H/м²

прямоугольник : τ _max = (3Q)/(2A)

круг: τ _max = (4Q)/(3A)

кольцо: τ _max = 2Q/A

Касательное напряжение при изгибе определяется по формуле Журавского: τ = (QS)/(bJ_x), H/м², где S - статический момент относительно нейтральной оси, м³, J_x – осевой момент инерции, м⁴

Расчеты на прочность при изгибе:

1. Проверочный расчет

Находится опасное сечение с M_max, Q _max

M_max→ σ_max≤[σ] -10%

Q _max→τ _max≤[τ] +5%

2. Проектный расчет

σ_max=M_max/W_x≤[σ]

W_x=M_max/ [τ]

прямоугольник: W_x=bh²/6

круг: W_x=0,2d³

Выполняются две проверки: f≤[f]

Ө≤[Ө]