П.3. Непрерывная св.

Функция распределения НСВ — непрерывная функция от х.

Пример: .

Можно дать более точное определение НСВ.

Def СВ X называют непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.

Аналогом закона распределения является плотность вероятности .

Функцию так же называют дифференциальной функцией распределения, существует только для НСВ.

Покажем вероятностный смысл плотности распределения:

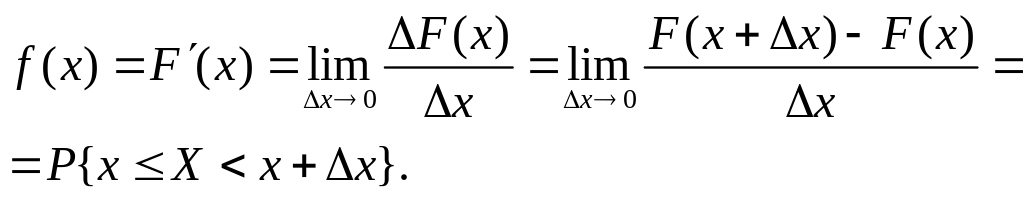
(по 4 свойству функции распределения).

Отношение представляет собой среднюю вероятность, которая приходится на единицу длины участка . Тогда . Т.е. плотность распределения есть предел отношения вероятности попадания СВ в промежуток к длине этого промежутка, когда она стремится к 0. Получаем:

. Или

.

Выражение называется элементом вероятности.

Свойства:

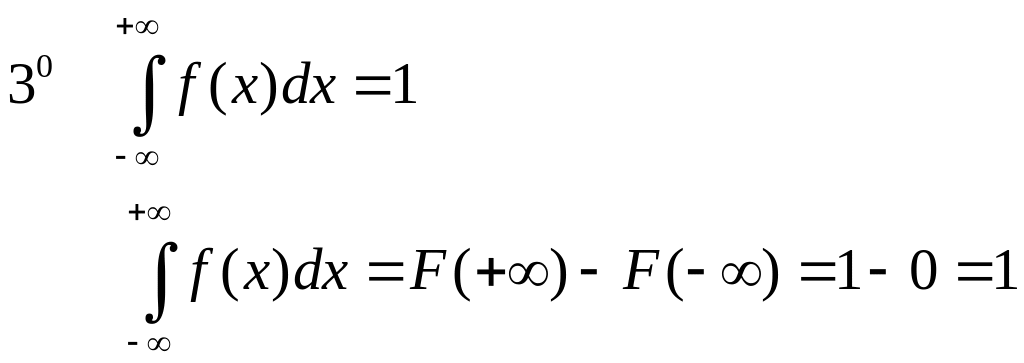
(Геометрически это означает, что площадь фигуры, ограниченной f(x) и осью абсцисс, равна 1).

Пример:

. Найти А, F(х), .

Решение:

.

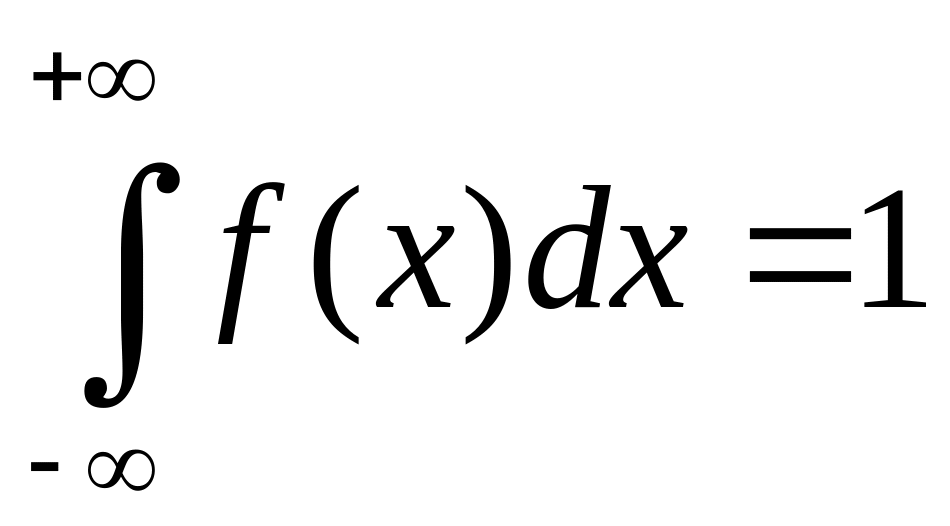
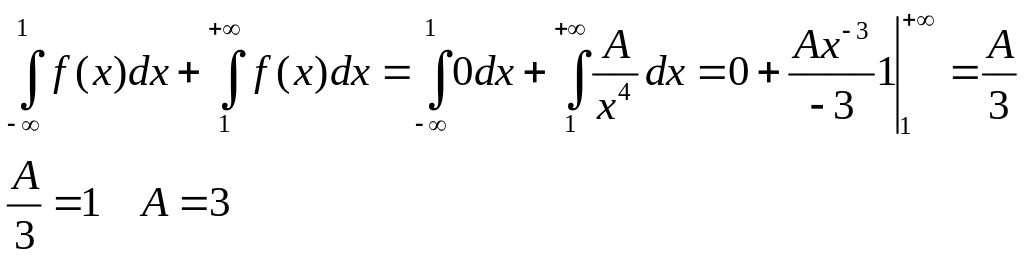
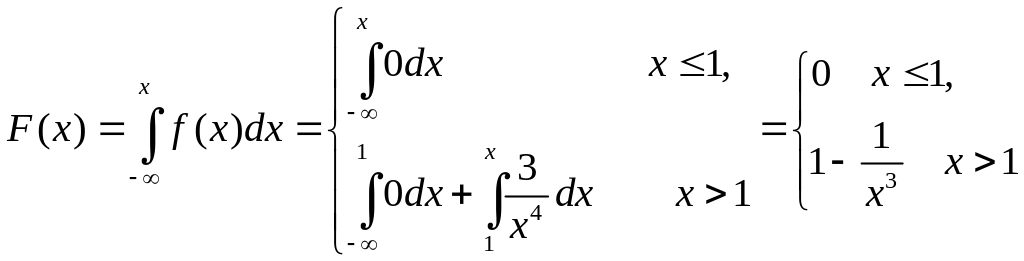или

Параграф 11. Числовые характеристики. П.1. Характеристики положения.

При решении многих практических задач достаточно знать некоторые числовые параметры, характеризующие отдельные существенные свойства закона распределения СВ. Их называют числовыми характеристиками СВ.

Характеристики положения это математическое ожидание, медиана, мода.

Мат. ожидание СВ Х представляет собой некоторое «средневзвешенное» число, вокруг которого группируются значения СВ.

Например, поступающий на работу интересуется средним заработком.

Обозначение:

Вычисление:

для ДСВ

для НСВ .

Свойства:

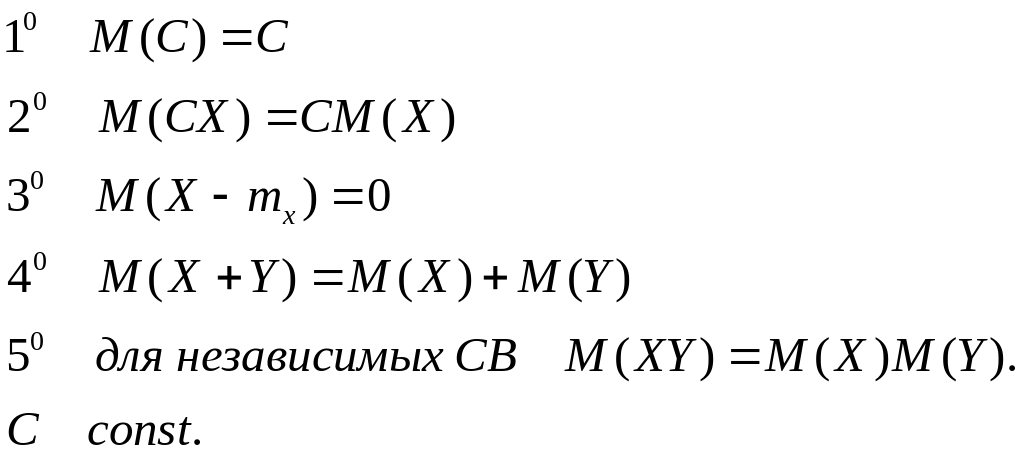
Матожидание имеет ту же размерность, что и СВ.

Def Модой ДСВ Х называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями. Обозначение:

Для НСВ Х — точка локального максимума плотности .

Если мода единственная, то распределение СВ называется унимодальным, если нет, то полимодальным:

Def Медианой НСВ Х называется такое ее значение для которого

Для ДСВ медиана обычно не определяется

П.2. Характеристики рассеивания.

Характеристики рассеивания: дисперсия, среднее квадратичное отклонение.

Дисперсия оценивает разброс возможных значений СВ относительно ее среднего значения (мат. ожидания). Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели.

Def Дисперсией СВ Х называется мат. ожидание квадрата разности между СВ Х и ее мат ожиданием.

.

Обозначение:

Вычисление:

для ДСВ

для НСВ .

Свойства:

Дисперсию удобнее считать по формуле .

Дисперсия имеет размерность квадрата СВ.

Когда нужно, чтобы оценка рассеивания имела ту же размерность что и СВ, используют с.к.о.

Def Средним квадратичным отклонением СВ Х называется корень квадратный из дисперсии

Пример: 1) Найти

	0	1	3	6
	0,1	0,5	0,3	0,1

или

2) СВ имеет плотность вероятности

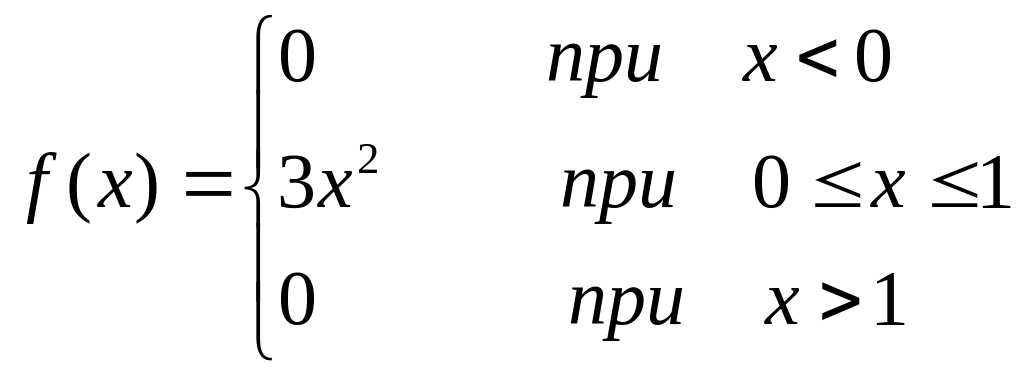
Найти
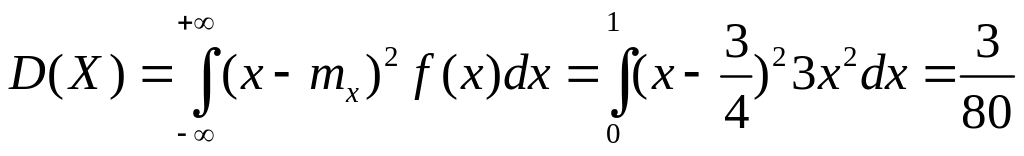