
- •Параграф 1. Введение
- •Параграф 2. Случайные события.
- •Параграф 3. Действия над событиями.
- •Параграф 4. Элементы комбинаторики.
- •Параграф 5. Различные определения вероятности. П.1 Классическое определение вероятности.
- •П.3 Геометрическое определение.
- •Параграф 6. Свойства вероятностей. Вероятность суммы и произведения событий.
- •Параграф 7. Формула полной вероятности. Формула Байеса.
- •Параграф 8. Повторение опытов. Схема Бернулли.
- •Параграф 9. Предельные теоремы теории вероятности. П.1 Теорема Пуассона.
- •П.2 Локальная предельная теорема Муавра-Лапласа.
- •П.3 Интегральная предельная теорема Лапласа.
- •Параграф 10. Случайные величины. П.1. Основные понятия.
- •П.2. Дискретная св.
- •П.3. Непрерывная св.
- •Параграф 11. Числовые характеристики. П.1. Характеристики положения.
- •П.2. Характеристики рассеивания.
Параграф 5. Различные определения вероятности. П.1 Классическое определение вероятности.
Существует простой способ определения вероятности события, основанный на равновозможности любого из конечного числа исходов опыта. Пусть проводится опыт с n исходами, которые можно представить в виде полной группы несовместных, равновозможных событий.
При рассмотрении событий естественно за единицу измерения принять вероятность достоверного события. Если приписать достоверному событию вероятность равную 1, то все другие события — возможные, но не достоверные, будут характеризоваться вероятностями, меньшими 1. Естественно, вероятность=0, приписать невозможному событию. Таким образом, диапазон изменения вероятностей любых событий — числа от 0 до 1. Итак, если F — достоверное событие, то P(F)=1; E —невозможное, то P(E)=0; A — случайное , то 0 <P(A)<1.
Def Вероятность события А это отношение числа благоприятных исходов к общему числу всех возможных исходов.
![]()
Пример: В урне 10 белых и 6 черных шаров. Какова
вероятность того, что наудачу вынутый шар окажется белым?
n – число всевозможных исходов. n=10+6=16. m – число благоприятных. m=10. Тогда
=![]()
П.3 Геометрическое определение.
Рассмотрим некоторую область U на которой выделена область А. Бросим на эту область иголку. Найти вероятность того, что точка попадет в область А.

лекция 2
Параграф 6. Свойства вероятностей. Вероятность суммы и произведения событий.
Сумма вероятностей противоположных событий равна 0.
 .
.Если
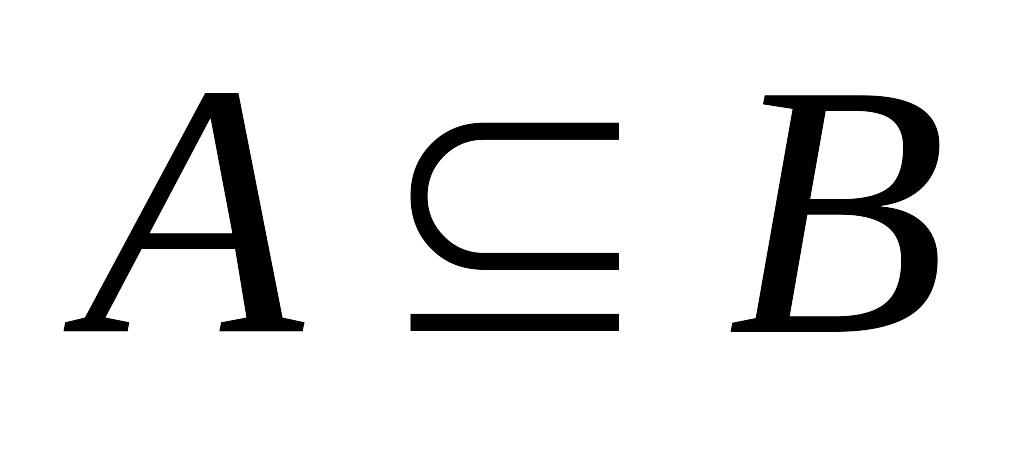 то
то
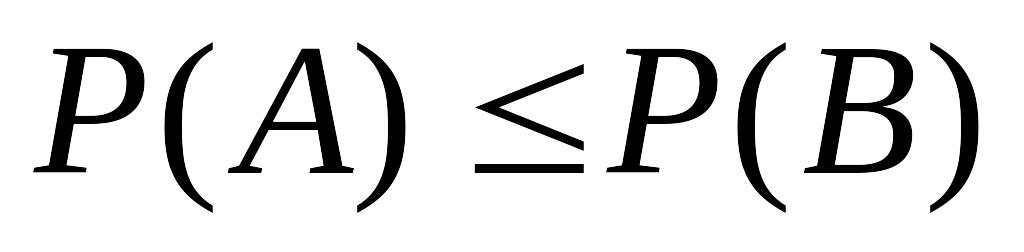 .
.Если события
 образуют полную группу несовместных
событий, т.е.
образуют полную группу несовместных
событий, т.е.
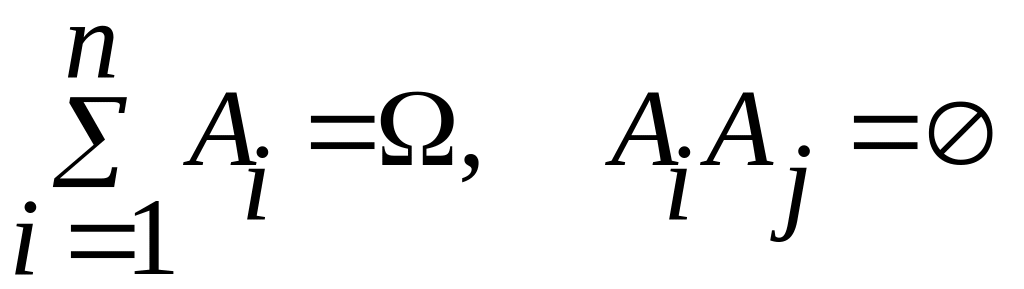 ,
то
,
то
 .
.
Пример: Наладчик наблюдает за 3 станками.
Вероятность того, что остановится 1-ый станок 0.2, Вероятность того, что остановится 2-ый станок 0.3, Вероятность того, что остановится 3-ый станок 0.4. Какова вероятность того, что остановится хотя бы один станок?

Найти вероятность того, что станки не остановятся.
![]() .
.
Теорема
Вероятность
произведения конечного числа независимых
событий равна произведению вероятностей
этих событий.
![]() .
.
Таким образом, можно дать другое определение независимых событий.
Def Два события называются независимыми, если появление одного из них не влияет на вероятность появления другого.
Теорема
Вероятность
суммы совместных событий равна
![]() .
.
Def
Вероятность осуществления события В
при условии, что событие А осуществилось
называют условной
вероятностью
В при условии А и обозначают
![]()
Теорема
Вероятность
произведения двух зависимых событий
равна произведению вероятности одного
из них на условную вероятность другого,
вычисленную в предположении, что первое
событие уже наступило:
![]() .
.
Для n зависимых событий справедлива формула

Пример: 1) В урне 2 белых и 3 черных шара.
Вынимают по одному 2 шара. Событие А — 1-ый вынутый шар белый, событие В — 2-ый вынутый шар белый.

2) найти вероятность того, что оба вынутых шара белые.
![]()
3) В коробке 8 пронумерованных шаров. Извлекают по одному 3 шара. Найти вероятность того, что последовательно появятся шары с номерами 5,6,7.
а) с возвращением в коробку,
в) без возвращения.
А — появление шаров 5,6,7
![]() — появление
шара 5
— появление
шара 5
![]() – появление
шара 6
– появление
шара 6
![]() — появление
шара 7
— появление
шара 7
![]()
а) События
независимые.
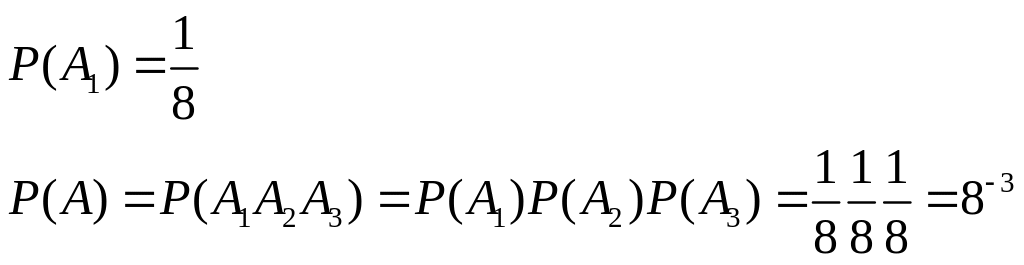
в) События зависимые
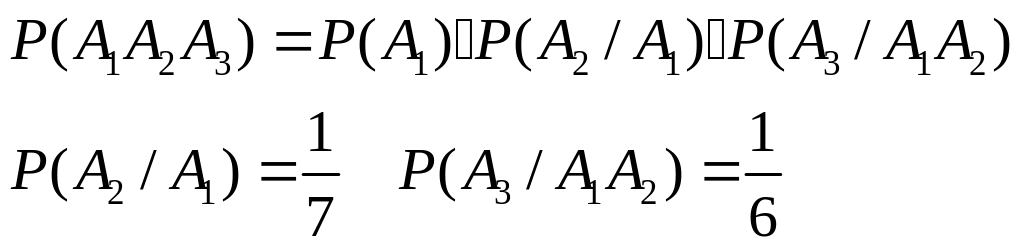
![]()
