
- •Задание 3
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 9
- •Задание 2
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 6
- •Задание 2
- •Задание 3
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 2
- •Задание 3
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
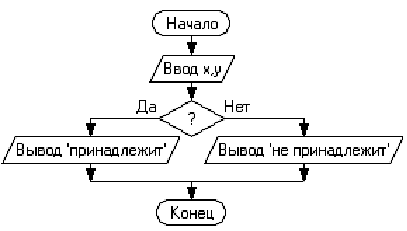
Задание 3
Приведенная блок-схема реализует
алгоритм …

-
□
поиска наибольшего значения из трех заданных чисел
□
поиска наименьшего значения из трех заданных чисел
□
определения имени переменной, хранящей наибольшее значение
□
определения имени переменной, хранящей наименьшее значение
Решение: Данной блок-схемой представлена алгоритмическая конструкция ветвления в полной форме. Первое условие сравнивает значения переменных А и В. Если значение А больше В, то выполняется сравнение значений А и С и наибольшее из них запоминается в переменной D. Если значение А меньше или равно В, то выполняется сравнение значений В и С и наибольшее из них запоминается в переменной D. Таким образом, переменная D будет хранить наибольшее из трех заданных значений.
Задание 4
 Даны
действительные числа
Даны
действительные числа
![]() ,
,
![]() и
схема алгоритма определения принадлежности
точки с координатами
,
заштрихованной
области на рисунке. В схеме не достает
проверки условия …
и
схема алгоритма определения принадлежности
точки с координатами
,
заштрихованной
области на рисунке. В схеме не достает
проверки условия …

-
□
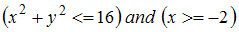
□

□

□
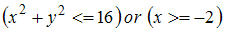
Решение:
Данный
алгоритм представлен в виде схемы,
содержащей ветвление. Для определения
принадлежности точки
![]() заштрихованной
области, указанной на рисунке, необходимо
составить сложное условие. Для этого
необходимо учесть все условия
принадлежности:
заштрихованной
области, указанной на рисунке, необходимо
составить сложное условие. Для этого
необходимо учесть все условия
принадлежности:
![]()
![]() Таким
образом, необходимое условие
Таким
образом, необходимое условие
Задание 5
 Алгоритм,
представленный данной блок-схемой,
возвращает значение …
Алгоритм,
представленный данной блок-схемой,
возвращает значение …
-
□
Истина, если верно утверждение трехзначное число n кратно каждой своей цифре, и Ложь – в противном случае
□
Истина, если верно утверждение трехзначное число n кратно хотя бы одной своей цифре, и Ложь – в противном случае.
□
логического произведения всех цифр числа
□
логической суммы всех цифр числа
Решение: Данный алгоритм является линейным. Это означает, что действия выполняются последовательно друг за другом в указанном порядке. Результатом действия А:=n mod 10 является целочисленный остаток от деления n на 10, то есть последняя цифра числа n. В действии В:=n div 100 находится целочисленный результат деления n на 100. В случае трехзначного числа это будет первая цифра числа n. Результатом действия С:=n div 10 mod 10 является вторая цифра числа, так как операции div и mod имеют одинаковый приоритет и выполняются слева направо. L присваивается значение логического выражения, которое принимает значение Истина только в том случае, когда истинно выражение в каждой скобке. В скобках проверяется остаток от деления исходного числа n на каждую цифру данного числа. Если все остатки от делений равны 0, выражения в скобках принимают значение Истина, и результатом всего логического выражения будет Истина. Таким образом, правильный ответ: возвращает значение Истина, если верно утверждение трехзначное число n кратно каждой своей цифре, и Ложь – в противном случае.
