Задание 6
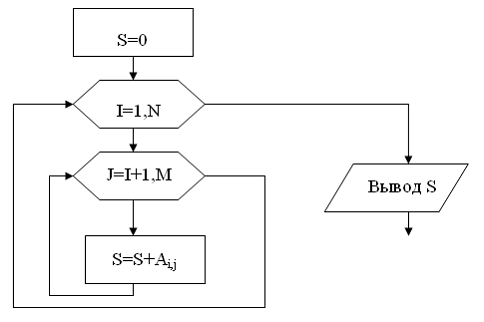
Дан массив А размерами NxM.
Приведенный алгоритм вычисляет сумму …
-
□
элементов матрицы, находящихся выше главной диагонали
□
элементов матрицы, находящихся на главной диагонали
□
всех элементов матрицы
□
элементов матрицы, находящихся ниже главной диагонали
Решение: Массив состоит из фиксированного числа элементов (компонент) одного типа и характеризуется общим именем. Доступ к отдельным элементам массива осуществляется с помощью общего имени и порядкового номера (индекса или адреса) необходимого элемента, например А[3] или А[i]. Для работы с элементами массива необходимо использовать цикл, с помощью которого будут перебираться все элементы. Матрица – это двумерный массив, каждый элемент которого имеет два индекса: номер строки – i; номер столбца – j. Причем при обращении к элементу матрицы А[i,j] первый индекс всегда обозначает номер строки, а второй – номер столбца. К любому элементу массива или матрицы можно обратиться с помощью его имени и индексов. Матрицы, как и массивы, нужно вводить, выводить и обрабатывать поэлементно. Обработка матрицы заключается в том, что вначале поочередно рассматриваются элементы первой строки (столбца), затем второй и т.д. до последней. В задачах обработки матриц используются следующие свойства матриц: – если номер строки элемента совпадает с номером столбца (i = j), то это означает, что элемент лежит на главной диагонали матрицы; – если номер строки превышает номер столбца (i > j), то элемент находится ниже главной диагонали; – если номер столбца больше номера строки (i < j), то элемент находится выше главной диагонали. – элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i+j-1 = n; – неравенство i+j-1 < n характерно для элемента, находящегося выше побочной диагонали; – элементу, лежащему ниже побочной диагонали, соответствует выражение i+j-1 > n. Алгоритм, представленный на блок-схеме, суммирует элементы, для индексов которых выполняется условие i < j. Итак, данный алгоритм вычисляет сумму элементов матрицы, находящихся выше главной диагонали.
Задание 7
Дан массив А размерами
N x M.
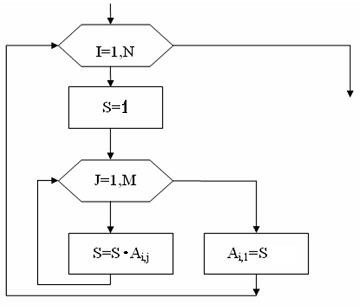Приведенный
алгоритм …
-
□
заменяет первый элемент каждой строки произведением элементов этой строки
□
вычисляет произведение всех элементов матрицы
□
вычисляет произведение элементов в столбцах матрицы
□
заменяет первый элемент каждого столбца произведением элементов этого столбца
Решение: Алгоритм, представленный блок-схемой, работает следующим образом. Внешний цикл задает номер строки i = 1,N. Внутренний цикл задает номер столбца j = 1,M. Так как при каждом значении i , переменная j пробегает все значения от 1 до М, то обработка массива происходит по строкам. В переменной S накапливается произведение элементов i строки. После окончания работы внутреннего цикла в первый элемент i строки заносится значение произведения элементов данной строки, значение S вновь приравнивается 1, и происходит переход на новую строку матрицы.