1.3 Электропроводимость в осадочных горных породах

Итак, осадочные горные породы состоят из породообразующих минералов и пустот (пор), заполненных водой, нефтью, газом или смесью этих флюидов. Большинство породообразующих минералов - кальцит, кварц, полевые шпаты, слюда - имеют очень большое сопротивление и практически не проводят электрического тока. Примесь в осадочной породе высокопроводящих рудных минералов (пирита, магнетита и др.) при содержании меньшем 5%, оказывает небольшое влияние на удельное сопротивление породы.

Осадочные горные породы, слагающие разрезы нефтяных и газовых месторождений, как правило, содержат менее 5 % рассеянных зерен рудных минералов. Однако, несмотря на весьма высокое сопротивление породообразующих минералов, удельное сопротивление различных осадочных пород в естественном залегании изменяется в широком диапазоне - от десятых долей Ом-метра до сотен тысяч (рис. 1.1).

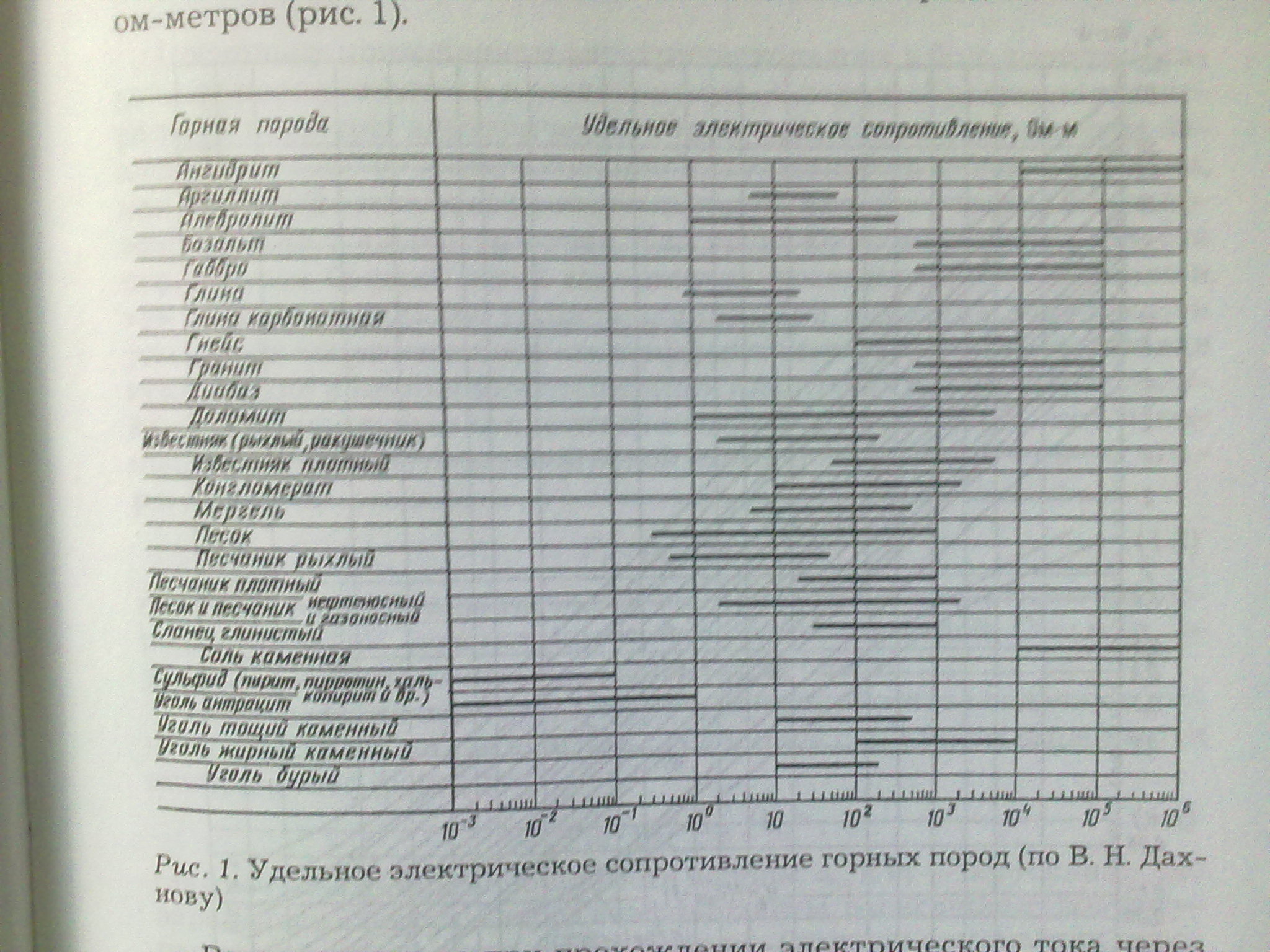
Рис. 1.1. УЭС горных пород (по В.Н. Дахнову)

Нефть, заполняющая пустоты породы, также обладает очень высоким сопротивлением (10⁹ - 10¹⁶ Ом м). Роль проводника при прохождении электрического тока через осадочные породы играет пластовая вода, содержащая растворенные соли. Размер удельного сопротивления породы в каждом отдельно взятом случае зависит от удельного сопротивления насыщающих поры породы пластовых вод; процентного содержания водных растворов и углеводородов в порах породы; текстурных особенностей породы; горного давления и температуры на глубине залегания. Удельное сопротивление пластовых вод, в свою очередь, зависит от концентрации, состава растворенных солей и температуры.

2. Физико-математическое моделирование электромагнитных процессов в горной породе

Физическое моделирование широко применяется в геологии и геофизике при изучении физических процессов, происходящих в горных породах. В петрофизике физическое моделирование осуществляют на образцах горных пород, отобранных в скважинах - керне. С помощью образцов моделируют процессы фильтрации флюидов, электромагнитные, тепловые, диффузные, ядерные, акустические и другие природные процессы. В некоторых случаях создают модели самих горных пород (искусственные образцы), на которых выполняют в последующем моделировании указанных процессов.

Кроме самих физических процессов, иногда моделируют термобарические условия, в которых протекают эти процессы. Для этой цели используют специальные установки, позволяющие моделировать температуру залегания горных пород, геостатическое и пластовое давление.

Проведение физического моделирования в петрофизике связано с большими трудностями:

1. Нарушение геометрического подобия натурного объекта и модели. Объем породы, исследуемый в лаборатории, не соответствует ее объему в природных условиях залегания, который изучается геофизическими методами в скважинных вариантах и особенно методами полевой (наземной) геофизики.

2. Изолированность модели. В природных условиях, в отличие от лабораторных, исследуемый объект занимает определенное пространственное положение среди других пород с иными литологическими и петрофизическими характеристиками, и находится с ними в физико-химическом и термодинамическом равновесии.

3. Несоответствие внутренней структуры пород первоначальной. При изменении температуры и давления от пластовых к поверхностным в образцах горной породы происходят ее изменения, связанные с дополнительной трещиноватостью, усыханием и растрескиванием глинистого материала, изменением порового объема породы за счет обратимых и необратимых деформаций ее скелета и т.д.

Математическое моделирование, часто используемое в петрофизике, позволяет изучать явления природы с помощью математических моделей, описывающих приближенно какой-либо их класс.

Процесс математического моделирования включает 4 этапа:

1. Формулирование законов, связывающих главные элементы модели, и запись в математической форме зависимостей между ними;

2. Решение прямой задачи - получение количественной информации;

3. Решение обратной задачи - определение характеристик модели и сопоставление выходной информации с результатами эксперимента;

4. Последующий анализ модели и построение новой, более совершенной математической модели.

По характеру воспроизводимых сторон объекта исследования различают моделирование его структуры (структурные модели), моделирование функционирования протекающих в нем процессов (функциональные модели) или же моделирование совместно структуры и физико-химических процессов объекта (смешанные модели).