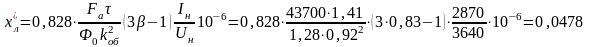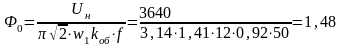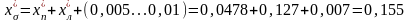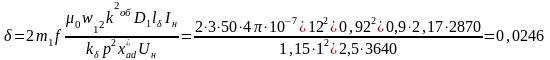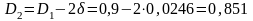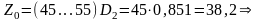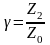1.3. Немагнитный зазор

Выбор величины зазора является одним из наиболее ответственных моментов при проектировании турбогенератора, так как от зазора зависят многие технико-экономические показатели. Зазор представляет собой основное магнитное сопротивление магнитной цепи, и с его ростом растут необходимая Н.С. обмотки возбуждения, масса обмотки возбуждения, потери на возбуждение и себестоимость турбогенератора. Так как ротор является наиболее нагруженной в тепловом и механическом отношении частью, то естественно стремление к уменьшению немагнитного зазора. С другой стороны, зазор определяет основной параметр турбогенератора – синхронное индуктивное сопротивление обмотки статора x_d, а также такие важные эксплуатационные характеристики, как отношение короткого замыкания (ОКЗ) и статическую перегружаемость S.

Для расчета величины воздушного зазора необходимо определить параметры обмотки статора.

Относительное значение индуктивного сопротивления пазового рассеяния, о.е.

(1.28)

.

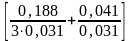
где размеры паза h₁₁, h₄, b_п1, – см. рис.1.6 –1.8;

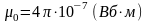– магнитная проницаемость вакуума;

для коэффициент, учитывающий уменьшение пазового рассеяния обмоток с укороченным шагом

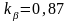
Относительное сопротивление лобового рассеяния, о.е.

(1.29)

где амплитуда н.с. статора на полюс, А,

(1.30)

Ф₀ – магнитный поток при холостом ходе и U = U_н , Вб,

(1.31)

Индуктивное сопротивление рассеяния обмотки статора в относительных единицах

(1.32)

где добавка (0,005…0,01) приближенно учитывает рассеяние по коронкам зубцов и дифференциальное рассеяние (большие значения для P_н < 6 МВт, при P_н > 100 МВт ею можно пренебречь).

Индуктивное сопротивление Потье в относительных единицах

(1.33)

Синхронное индуктивное сопротивление взаимоиндукции x_ad^* в о.е. определяется по значению сопротивления Потье для заданного коэффициента мощности по рис. 1.12.

После определения x_ad^* можно рассчитать величину воздушного зазора, м,

(1.34)

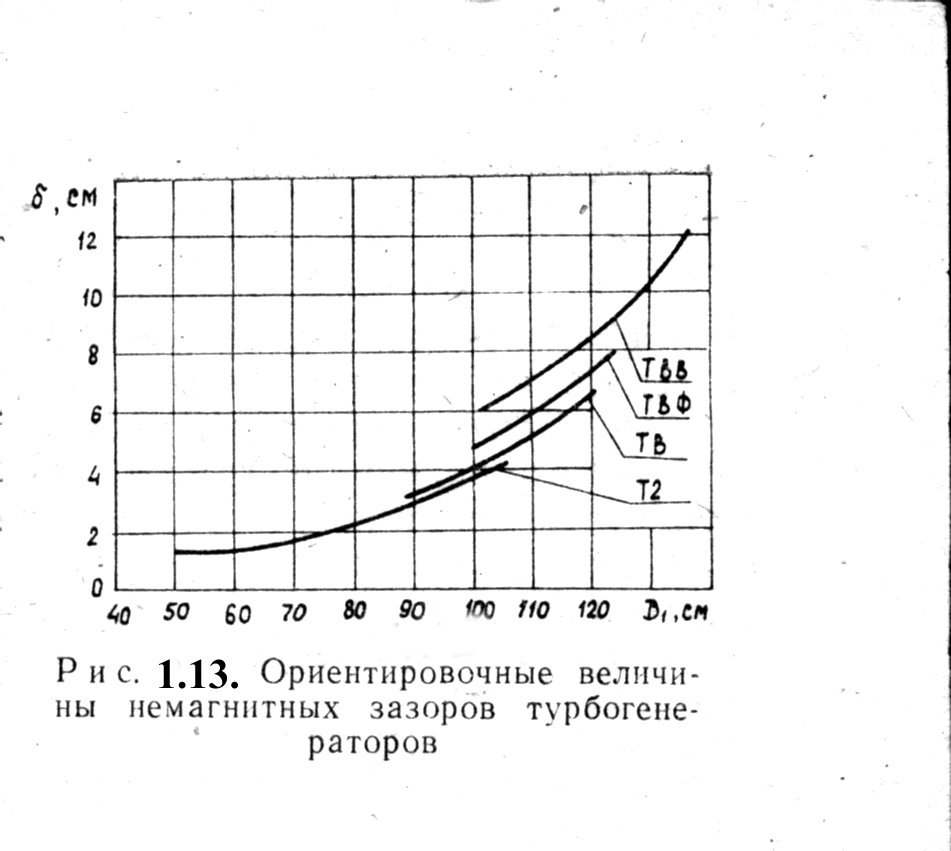
Рис. 1.13. Ориентировочные величины магнитных зазоров турбогенераторов

где k_ - коэффициент воздушного зазора, который может быть предварительно принят равным 1,1…1,15 для мощностей более 25 МВт и 1,15… 1,2 для меньших мощностей.

Полученное значение величины воздушного зазора следует сравнить со средними величинами, представленными на рис. 1.13.

ГЛАВА ВТОРАЯ

Основные размеры и

обмоточные данные ротора

2.1. Основные размеры зубцово-пазовой зоны.

Ротор является наиболее нагруженным в тепловом и механическом отношении узлом турбогенератора. Во-первых, из-за механических напряжений, возникающих в зубцах ротора, и особенно в бандажах, диаметр ротора ограничен величиной 1,2 м. Во-вторых, все турбогенераторы проектируются для работы в режиме перевозбуждения, при котором н.с. должна равняться сумме продольной составляющей н.с. реакции якоря и н.с. магнитной цепи с большим немагнитным зазором. Поэтому линейная нагрузка ротора должна превышать линейную нагрузку статора в 1,5 – 1,7 раза. Однако из-за ограниченной глубины пазов линейная нагрузка может быть увеличена только за счет увеличения плотности тока в обмотке ротора, которая может превышать плотность тока обмотки статора в 1,3 –2 раза. При этом возможности охлаждения ротора невелики из-за ограниченных размеров и его монолитности. Температурные ограничения при росте мощности и степени использования турбогенераторов наступают быстрее для ротора, чем для статора.

Внешний диаметр ротора, м

(2.1)

Активная длина ротора обычно выбирается немного большей, чем действительная длина статора, м:

(2.2)

В мощных и высокоиспользованных турбогенераторах l₂ = l_ .

При расчете зубцового слоя ротора обычно вначале задаются числом фиктивных пазов Z₀ по всей окружности ротора

(2.3)

Для получения оптимальной величины

(2.4)

обеспечивающей максимальное приближение распределения поля возбуждения к синусоидальному, значения Z₀ и Z₂ выбираются по таблице 2.1.

Z0	20	24	28	32	38	42	46	52	54
Z2	12	16	20	24	28	32	36	40	40
	0,6	0,666	0,71	0,75	0,737	0,762	0,782	0,769	0,74
()	12,8	6,16	5,5	7,4	6,55	8,1	9,8	8,8	6,6

Таблица 2.1 Оптимальные соотношения пазов ротора.

Относительную высоту паза ротора ₂ и относительную площадь фиктивного числа пазов ротора S₀ можно найти по точкам пересечения прямой и семейства кривых рис.3.1 и 3.2.

Высота паза ротора, м

(2.5)

ГРАФИКИ ОПТИМАЛЬНЫХ РАЗМЕРОВ

ПАЗОВ РОТОРОВ

а его ширина

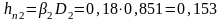
(2.6)

Эти размеры следует считать предварительными, так как после размещения в пазах ротора целого числа нормализованных по размерам поперечного сечения проводников и изоляции возможна некоторая корректировка h_п2 и b_п2.