23.Метод минимальных путей и сечений

Метод минимальных путей и сечений

Этот метод применяется только для систем с монотонной структурой, свойства которых формулируются следующим образом:

• система работоспособна, если все элементы работоспособны;

• система находится в состоянии отказа, если все элементы отказали;

• при отказе элемента состояние системы только ухудшается.

Минимальный путь – это такое множество элементов, при нормальной работе которых система работоспособна, а отказ любого из этих элементов приводит к отказу системы.

Минимальное сечение – это такое множество элементов, отказ которых приводит к отказу системы, но работоспособное состояние любого из них обеспечивает работоспособное состояние системы при условии работоспособности элементов, не входящих в данное минимальное сечение.

В общем случае система может иметь несколько минимальных путей и минимальных сечений. Любую структурную схему можно представить в виде параллельного соединения минимальных путей или в виде последовательного соединения минимальных сечений. Только система из последовательно соединенных элементов имеет единственный минимальный путь.

Этот метод дает не точные значения показателей надежности, а граничные (интервальные) оценки этих показателей сверху и снизу. Во многих случаях, особенно для сложных систем, подобных оценок оказывается достаточно.

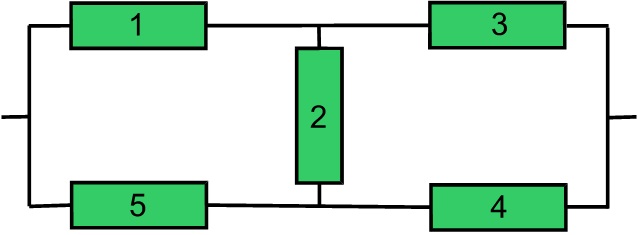
Сначала определяем минимальные пути для анализируемой схемы. Множество элементов, работоспособность которых обеспечивает работоспособность системы, следующие: {13}, {54}, {124}, {523}, {134}, {543}, {153}, {154}, {524}, {123}, {1524}, {1523}, {1234}, {5234}, {1354}, {15234}. Из них минимальными являются пути: 13, 54, 124, 523. Количество минимальных путей – 4.

Вероятность безотказной работы такого соединения элементов дает оценку «сверху» вероятности безотказной работы исходной системы:

PB = 1 – (1 – p1p3)⋅(1 – p5p4)⋅(1 – p1p2p4)⋅(1 – p5p2p3)≈0,997.

Затем выделим минимальные сечения, т.е. такие варианты цепочек элементов, которые при отказе всех элементов цепочки дают отказ всей системы, несмотря на работоспособность остальных цепочек. Значит, цепочки соединены между собой последовательно, а поскольку при работоспособности любого из элементов внутри цепочки она обеспечивает работоспособность всей системы (при исправности остальных цепочек), то, следовательно, элементы в пределах цепочек соединены параллельно. Набор минимальных сечений выглядит следующим образом:

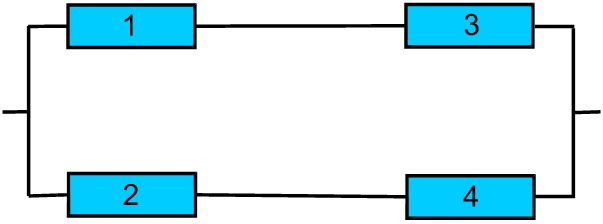
Вероятность безотказной работы набора минимальных сечений дает оценку «снизу» вероятности безотказной работы схемы.

PН = (1 – q1q5)⋅(1 – q3q4)⋅(1 – q1q2q4)⋅(1 – q5q2q3)

При вероятности отказа любого элемента схемы q=1 – p=0,1 получаем оценку снизу PН ≈ 0,978.

Обратим внимание, что PН ≈ 0,978 совпадает с результатом вычисления вероятности безотказной работы системы по приведенным ранее точным методам (метод перебора состояний и метод разложения относительно особого элемента).

Таким образом, согласно методу минимальных путей и сечений, оценка вероятности безотказной работы рассматриваемого соединения при заданных значениях показателей надежности его элементов находится в пределах

0,978 ≤ PC ≤ 0,997.