27) Выбор оптимальных вариантов электроснабжения с учетом надежности.

При проектировании и эксплуатации систем электроснабжения одним из важнейших критериев является экономичность, т.е. снижение издержек на эксплуатацию системы. Оптимальность проектного решения при этом означает, что заданный производственный эффект (располагаемая мощность, уровень надежности электроснабжения и качества электроэнергии получается при минимально возможных за-

тратах материальных ресурсов.

При определении оптимального варианта из некоторого числа

возможных, обеспечивающих выполнение технического задания, не-

обходимо вычислить приведенные затраты на сооружение и эксплуа-

тацию энергетического объекта, которые в зависимости от длительно-

сти сооружения и условий поочередного ввода исчисляются по-

разному.

Если строительство и пуск в эксплуатацию осуществляются в

течение одного года, то:

З = рн. *К + И , (6.17)

где рн. – нормативный коэффициент эффективности кап. вложений К

(в энергетике, при нормативном сроке службы 8 лет, рн. = 1/8 = 0,12 );

И – годовые издержки, руб.

Если объект строится на протяжении Т лет, то:

где рн.п. – нормативный коэффициент приведения разновременных

затрат, определяемый финансовой политикой государства для каждой

отрасли (в энергетике );

Kt – капитальные вложения в t -м году, руб.;

τ – год приведения затрат (чаще всего затраты приводят к пер-

вому году периода T или к году окончания строительства).

Если в период многолетнего строительства вновь созданные ос-

новные фонды частично эксплуатируются (например, при поэтапном

развитии систем электроснабжения), то:

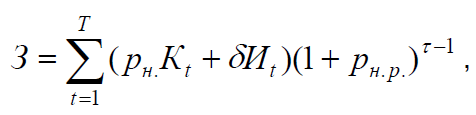
где δИt – приращение издержек в t -м году по сравнению с (t −1) .

Оптимальным вариантом считается такой, у которого приведен-

ные затраты, определяемые по формулам (6.17)... (6.19), минимальны.

Однако сравниваемые варианты могут отличаться по степени надеж-

ности. Несоблюдение условия одинаковой надежности или качества в

сравниваемых вариантах приводит к нарушению основного требова-

ния – равенства экономического эффекта.

При сравнении подобных вариантов с неодинаковой надежностью

необходимо вводить в расчетные формулы члены, учитывающие воз-

можный экономический ущерб от отказов оборудования и установок,

или члены, учитывающие затраты на повышение надежности до норма-

тивного уровня. В этом случае формулы (6.17)...(6.19) примут вид:

З = рн. * К + И +У ; (6.20)

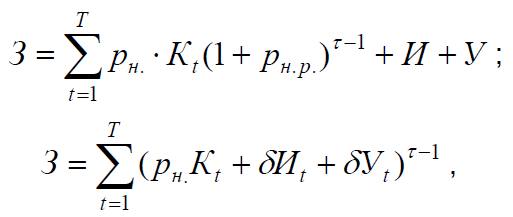
где У – средний годовой народнохозяйственный ущерб на стадии

нормальной эксплуатации;

δУt – приращение издержек в t -м году и (δУt =Уt –Уt).

Окончательный вариант проектного решения определяется пу-

тем комплексного технико-экономического сравнения (по критериям

надежности и экономичности). При этом практически неразличимыми

считают варианты, у которых значения рн. ⋅ К + И различаются ме-

нее, чем на 5%, а значения У – менее, чем на 10% [11]. Уверенное

различение вариантов по затратам с учетом ущерба начинается при

различии оценок затрат не менее чем на 15%. При различии оценок

затрат с учетом ущерба на 5-15% вероятность ошибки при выборе со-

ставляет 10-20%, т. е. весьма существенна.

92

При попарном сравнении вариантов возможны следующие случаи:

а) Варианты неразличимы по показателю У (попадают в зону

равной надежности):

но различимы по затратам без учета ущерба – по (6.17). В этом случае

при условии

( рн.К2 + И2 ) − ( рн.К1 + И1) >> 5%

вариант №1 считается лучшим, чем вариант №2.

б) Варианты неразличимы по затратам без учета ущерба (в зоне

равной экономичности):

( рн.К2 + И2 ) − ( рн.К1 + И1) ≤ 5%,

но различимы по ущербу. В этом случае при условии У2 −У1 >> 5%

вариант №1 лучше, чем вариант №2.

в) Варианты различаются по затратам без учета ущерба и по

ущербу:

( рн.К2 + И2 ) − ( рн.К1 + И1) >> 5%;

В этом случае проверяется условие:

( рн.К2 + И2 +У2) − ( рн.К1 + И1 +У1) > 0 .

Если неравенство выполняется, то вариант №1 признается лучшим,

чем вариант №2.

г) Варианты неразличимы ни по ущербу, ни по затратам, т.е. на-

ходятся в зоне неопределенности интегральных критериев надежно-

сти и экономичности:

( рн.К2 + И2 ) − ( рн.К1 + И1) ≤ 5%;

В этом случае варианты сравнивают по другим техническим критери-

ям (потерям электроэнергии, удобству монтажа и обслуживания, воз-

можности модернизации и т.д.)

Следует отметить, что все выше приведенные критерии исходи-

ли из предположения, что величина ущерба У – детерминированная,

т.е. определенная для любых условий. Только при этом условии мож-

но находить максимумы, минимумы, проверять условия равенства или

неравенства.

В действительности, как это следует из предыдущих глав, вели-

чина У – случайная, и позволяет прямо использовать критерии опти-

мизации. В математической статистике для ухода от подобной неоп-

ределенности случайную величину заменяют ее средним значением

У , но при этом остается риск, что фактический ущерб окажется

больше среднего, и это превышение характеризуется величиной

среднеквадратического отклонения σ (У) .

Если субъект экономики (энергоснабжающее предприятие) де-

лает какие-то затраты на обеспечение надежности, то он должен быть

уверен в их оправданности с учетом ожидаемого риска. Таким обра-

зом, расчетные затраты следует записывать в виде:

94

З = З + Цр *σ (У) = рн.К + И +У + Цр *σ (У) , (6.23)

где Цр - цена риска, которая зависит от того, каким ресурсным потен-

циалом обладает субъект, принимающий решение.

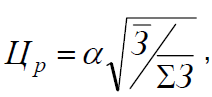
где α характеризует допускаемую степень риска (α = 3...4 );

ΣЗ - средний годовой располагаемый ресурс предприятия.

В случае, если все экономические решения принимаются госу-

дарством или от имени государства (пример – РАО «ЕЭС»), то вели-

чина ΣЗ очень велика по сравнению с затратами по какому-то кон-

кретному объекту, и цена риска приближается к нулю. На этом осно-

вании во всех расчетах вполне допустимо пользоваться средними

значениями ущерба, как в выражениях (6.20)-(6.22).

Однако в современной многоукладной экономике много хозяйст-

вующих субъектов, распоряжающихся гораздо меньшими ресурсами,

для которых важно учитывать экономические риски и использовать

различные страховые механизмы.

Если считать случайную величину ущерба распределенной по

нормальному закону, то при σ (У) ≤ 0,3У то с достоверностью 0,999

можно принять Цр = 3 ; а с достоверностью 0,99997 Цр = 4 . Если же

σ (У) ≈У , то достоверность 0,999 обеспечивается при Цр ≈ 7 ; а дос-

товерность 0,9999 при Цр ≈ 9 .