Элементы геометрии Лобачевского

I. «Начала» Евклида. Пятый постулат Евклида

Евклид (330-275 г.г. до н.э.) «Начала»

13 книг: 14, 6 книги  планиметрия; 1113 книги  стереометрия; остальные  арифметика в геометрическом изложении.

В каждой книге: понятия; постулаты; аксиомы; предложения (теоремы и задачи на построение).

Примеры:

Определение 1: Точка есть то, что не имеет частей.

Определение 2: Линия есть длина без ширины.

Определение 3: Прямая есть такая линия, которая одинаково расположена по отношению ко всем своим точкам.

Постулат I: Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую.

Постулат IV: Все прямые углы являются равными друг другу.

Постулат V: Требуется, чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.

Утверждения, с помощью которых можно было бы доказать V постулат Евклида:

1. Все перпендикуляры к одной стороне некоторого острого угла пересекают его другую сторону.

2. Существуют подобные и неравные треугольники.

3. Существуют треугольники сколь угодно большой площади.

4. Существуют треугольники с суммой углов, равной двум прямым.

5. Через точку вне данной прямой можно провести не более одной прямой, ей параллельной.

Многие геометры заменяли V постулат Евклида его отрицанием или утверждением, эквивалентным отрицанию V постулата.

Саккери Джироламо (16671733 г.г.)  итальянский математик, создатель первого наброска неевклидовой геометрии.

Ламберт Иоганн Генрих (17281777 г.г.)  физик , философ, математик.

Лежа́ндр Адриен Мари (17521833 г.г.)  французский математик.

Лобачевский Николай Иванович (17921856 г.г.)  русский математик, создатель неевклидовой геометрии (1826 г.).

Бо́йяи Я́нош (18021860)  венгерский математик, один из первооткрывателей неевклидовой геометрии (называемой теперь геометрией Лобачевского).

Поддержали работу Лобачевского:

Га́усс Иоганн Карл Фри́дрих (17771855)  немецкий математик, астроном и физик.

Бельтра́ми Эудженио (18351900)  итальянский математик. Сыграл значительную роль в признании неевклидовой геометрии.

Пуанкаре́ Жюль Анри́ (18541912)  французский математик, физик, астроном и философ.

Клейн Феликс Христиан (18491925)  немецкий математик и педагог.

II. Геометрия (планиметрия) Лобачевского

II.1. Параллельные прямые по Лобачевскому

Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского (АПЛ): Пусть a  произвольная прямая, A  точка, не лежащая на прямой a. Тогда в плоскости, определяемой точкой A и прямой a, существует не менее двух прямых, проходящих через A и не пересекающих прямую a.

Для иллюстрации аксиомы о параллельности прямых рассмотрим следующую схему:

Имея прямую a и точку A вне ее, соединяем A с точкой P, лежащей на a, и отодвигаем точку P в положение P', P'', ... и все дальше, и дальше на a (иными словами, представляется последовательность точек P, P', P'', ... или соответственно последовательность прямых AP, AP', AP'', ...). Прямая AP при этом вращается вокруг A и достигнет некоторого предельного положения, когда P удалится в бесконечность, и эту предельную прямую и надо понимать как прямую, параллельную прямой a, проходящую через A.

При этом нет никаких изначальных соображений, в силу которых прямая AP должна приближаться к одному и тому же предельному положению при удалении P в бесконечность как в одну, так и в другую сторону, что дает абстрактную возможность существования двух различных прямых, проходящих через A, параллельных прямой a. В этой связи постулат параллельных прямых в евклидовой геометрии – не что иное, как соглашение о том, что эти два предельных положения должны совпадать, и через точку A должна проходить только одна прямая, параллельная прямой a.

ДОКАЖИТЕ:

Следствие АПЛ: Пусть a  произвольная прямая, A  точка, не лежащая на прямой a. Тогда в плоскости, определяемой точкой A и прямой a, существует бесконечное множество прямых, проходящих через A и не пересекающих прямую a.

Замечание: В отличие от геометрии Евклида в геометрии Лобачевского параллельными к данной прямой называются только некоторые прямые из тех, которые не пересекают данную прямую.

Условимся считать: все рассматриваемые прямые являются направленными прямыми. Если прямая обозначена буквами AB, то A предшествует B. Рассматриваемые нами точки на этой прямой лежат между точками A и B (так выбираем эти точки).

О пределение: Прямая AB называется параллельной прямой CD, если эти прямые не имеют общих точек и для любых точек P и Q, лежащих соответственно на прямых AB и CD, любой внутренний луч (с вершиной  в вершине угла, целиком принадлежащий внутренней части угла) угла QPB пересекает луч QD.

Теорема 1 (признак параллельности прямых): Если прямые AB и CD не имеют общих точек и существуют точки P и Q, такие, что PAB, QCD, и любой внутренний луч угла QPB пересекает луч QD, то AB || CD.

Доказательство: Для доказательства достаточно установить, что для любых точек PAB, QCD, удовлетворяющих условию теоремы, любой внутренний луч h угла QPB пересекает луч QD.

Рассмотрим случаи:

1) P = P, Q  точка луча QC.

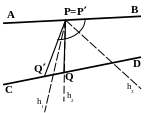
Угол QPB является объединением углов QPQ и QPB, следовательно, луч h либо лежит внутри угла QPQ, либо совпадает с лучом PQ, либо лежит внутри угла QPB. В первом и во втором случаях луч h пересекает отрезок QQ, т.е. пересекает луч QD. В третьем случае луч h по условию теоремы пересекает луч QD, следовательно, пересекает луч QD.

2) P = P, Q  точка луча QD.

Угол QPB является частью угла QPB, т.е. луч h лежит внутри угла QPB, следовательно, по условию теоремы h пересекает луч QD.

Луч h не проходит внутри угла QPQ, т.е. не пересекает отрезок QQ, следовательно, пересекает луч QD.