Пример №1
Найти
условный экстремум функции 
при
условии 
.
Решение
Геометрическая
интерпретация данной задачи такова:
требуется найти наибольшее и наименьшее
значение аппликаты плоскости 
для
точек ее пересечения с цилиндром
.
Выразить одну переменную через другую из уравнения связи и подставить ее в функцию несколько затруднительно, поэтому будем использовать метод Лагранжа.
Обозначив 
,
составим функцию Лагранжа:
.
Запишем систему уравнений для определения стационарных точек функции Лагранжа:
Если
предположить 
,
то первое уравнение станет таким: 
.
Полученное противоречие говорит о том,
что 
.
При условии
из
первого и второго уравнений имеем: 
.
Подставляя полученные значения в третье
уравнение, получим:
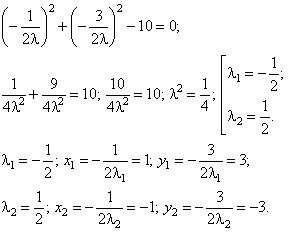
Итак,
система имеет два решения: 
, 
, 
и 
, 
, 
.
Выясним характер экстремума в каждой
стационарной точке: 
и 
.
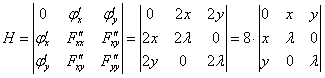
Для этого вычислим гессиан в каждой
из точек.
В
точке
получим:
,
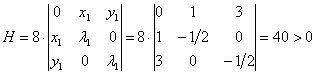поэтому в точке
функция
имеет условный максимум, 
.
Аналогично,
в точке
найдем: 
.
Так как
,
то в точке
имеем
условный минимум функции
,
.
Вопрос о характере экстремума в стационарных точках и можно решить и без использования гессиана. Определим знак в каждой стационарной точке:
При , поэтому функция имеет в точке условный максимум. Аналогично, в точке получим условный минимум функции . Отметим, что для определения знака не пришлось учитывать связь между dx и dy, ибо знак очевиден без дополнительных преобразований. В следующем примере для определения знака уже будет необходимо учесть связь между dх и dу.
24.1 Абстрактная теория рядов Фурье.
24.2 Тригонометрический ряд Фурье.
ригонометрическим
рядом Фурье функции 
называют функциональный
ряд вида
|
(1) |
где
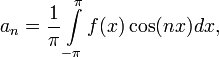
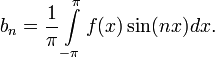
Числа 
,
и 
(
)
называются коэффициентами Фурье
функции
.
Формулы для них можно объяснить следующим
образом. Предположим, мы хотим представить
функцию
в
виде ряда (1), и нам надо определить
неизвестные коэффициенты
,
и
.
Если умножить правую часть (1) на 
и
проинтегрировать по промежутку 
,
благодаря ортогональности в правой
части все слагаемые обратятся в нуль,
кроме одного. Из полученного равенства
легко выражается коэффициент 
.
Аналогично для 
Ряд
(1) сходится к функции
в
пространстве 
.
Иными словами, если обозначить
через 
частичные
суммы ряда (1):
,
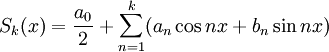то их среднеквадратичное отклонение от функции будет стремиться к нулю:
.
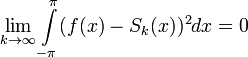25.1 Ядра Дирихле.
Ядро
Дирихле — 
-периодическая
функция, задаваемая следующей формулой:
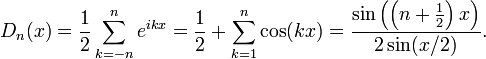
Функция
названа в честь французско-немецкого
математика Дирихле. Данная функция
является ядром, свёртка с которым
даёт частичную сумму тригонометрического ряда
Фурье. Это позволяет аналитически
оценивать соотношения между исходной
функцией и ее приближениями в
пространстве 
.
Соотношение с рядом Фурье
Пусть
—
интегрируема на
и
-периодическая,
тогда 
Эта формула является одной из важнейших в теории рядов Фурье.
Доказательство
Рассмотрим n-ную частичную сумму ряда Фурье.
Применяя формулу разности косинусов к выражению, стоящему под знаком суммы, получим:
Рассмотрим
сумму косинусов: 
Умножим
каждое слагаемое на 
и
преобразуем по формуле 
Применяя это преобразование к формуле (4), получим:
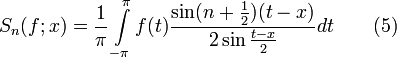
Сделаем
замену переменного 
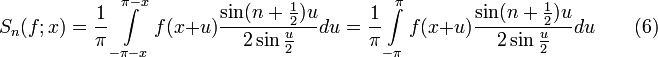
Свойства ядра Дирихле
—
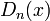функция
-периодическая
и четная.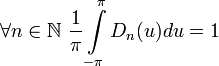
25.2 Условие сходимости рядов Фурье.
Интеграл Дирихле позволяет свести вопрос о сходимости ряда Фурье к вопросу о равенстве нулю интеграла
.
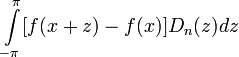Лемма
1. Если функция 
является
суммируемой на отрезке 
,
то
.
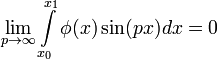Теорема
1. Если
—
суммируемая функция и при фиксированном
и
некотором 
существует
интеграл
,
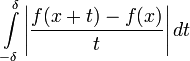то частичные
суммы 
ряда
Фурье функции
сходятся
в точке
к
.
Условие существования интеграла
для некоторого называется условием Дини.
26 Эвристический вывод преобразования Фурье.
27 Теорема Котельникова.
Теоре́ма
Коте́льникова (в англоязычной— теорема
Найквиста — Шеннона или теорема
отсчётов) гласит, что, если аналоговый
сигнал 
имеет
финитный (ограниченный по ширине) спектр,
то он может быть восстановлен однозначно
и без потерь по своим отсчётам, взятым
с частотой, строго большей удвоенной
верхней частоты 
:
Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временно́й характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой ».
Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и обычно имеют разрывы во временно́й характеристике. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают два следствия:
Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой , где — максимальная частота, которой ограничен спектр реального сигнала.
Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.
Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал можно представить в виде интерполяционного ряда
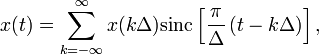
где 
—
функция sinc. Интервал дискретизации
удовлетворяет ограничениям 
Мгновенные
значения данного ряда есть дискретные
отсчёты сигнала 
.