20.2 Свойства непрерывных отображений

• Полный прообраз любого открытого (замкнутого) множества при непрерывном отображении — открытое (замкнутое) множество

• Образ компактного множества при непрерывном отображении — компактное множество.

• Непрерывная числовая функция на компактном множестве ограничена и достигает своих верхней и нижней граней. Это свойство следует из предыдущего.

• Образ связного множества при непрерывном отображении - связное множество.

• (Теорема Титце.) Любая вещественнозначная непрерывная функция, определённая на замкнутом подмножестве нормального пространства может быть продолжена до непрерывной функции на всё пространство.

• Сумма, разность и композиция непрерывных отображений также являются непрерывными отображениями.

• Из непрерывности линейного отображения одного линейного топологического пространства в другое следует его ограниченность. В случае нормированных пространств непрерывность линейного отображения эквивалентна ограниченности.

• Теорема Стоуна-Вейерштрасса (обобщение классической теоремы Вейерштрасса). Пусть 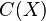 - пространство непрерывных функций на компактном хаусдорфовом топологическом пространстве 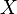 . Пусть 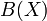  - подмножество  , содержащее константы, замкнутое относительно композиции и линейной комбинации функций, а также содержащее пределы своих равномерно сходящихся последовательностей функций. В таком случае 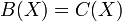  тогда и только тогда, когда 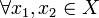 , существует 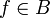 , такая что  .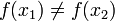

21.1

Дифференциалом отображения   в точке   называют линейный оператор   такой, что выполняется условие

21.2

Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.  При этом  Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx,  где α(Δx) - бесконечно малая функция, при Δx→0.  для функции одной переменной существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.Теорема 6 (необходимое условие дифференцируемости). Если функция дифференцируема в точке , то она имеет в точке частные производные по каждой переменной и .  При этом ,, где и – числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде  а полный дифференциал функции – в виде  Обратная теорема не верна, т.е. существование частных производных не является достаточным условием дифференцируемости функции.

21.3 Цепное правило дифференцируемости суперпозиции.

Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).

Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:

.

Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f₁(y₁),y₁ = f₂(y₂), …, y_n-1 = f_n(x), то

21.4-5 Производная по направлению и градиент.

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию   от   аргументов в окрестности точки  . Для любого единичного вектора   определим производную функции   в точке   по направлению   следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора  .

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.