Различные формы остаточного члена

В форме Лагранжа:

В форме Коши:

В интегральной форме:

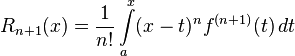
Ослабим предположения:

• Пусть функция   имеет   производную в некоторой окрестности точки 

• И   производную в самой точке  , тогда:

 — остаточный член в асимптотической форме (в форме Пеано, в локальной форме)

13.2 Формула Маклорена для элементарных функций.

13.3 Формула Тейлора с остатком Пеано.

14.1 Условие выпуклости функции.

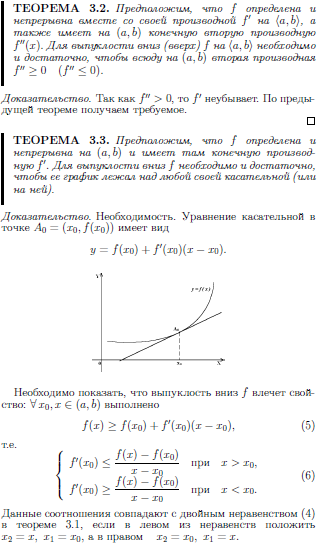
14.2 Исследование графиков функций.

15.1 Интегрирование простых дробей.

15.2 Интегрирование правильных дробей.

16.1 Схема построения интеграла Римана.

Пусть на отрезке   определена вещественнозначная функция  .

Рассмотрим разбиение отрезка   — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок   на n отрезков  . Длина наибольшего из отрезков   называется шагом разбиения, где  -длина элементарного отрезка.

Отметим на каждом отрезке разбиения по точке  . Интегральной суммой называется выражение  .

Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора  , то это число называется интегралом функции   на отрезке  , т.е.  .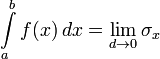

В этом случае, сама функция   называется интегрируемой (по Риману) на  ; в противном случае   является неинтегрируемой (по Риману) на отрезке  .

16.2 Необходимое условие интегрируемости функции одной переменной.

 Если функция интегрируема по области D, она ограничена в этой  

области.                      

Доказательство. (от противного)

Интегрируемая на [a,b] функция f не ограничена и зафиксируем некоторое разбиение τ={xi}i=ki=0. В силу неограниченности f на [a,b] она будет по крайней мере неограниченной на одном отрезке разбиения τ, например, на [x0,x1], тогда на этом отрезке существует последовательность ξ1n∈[x0,x1],n=1,∞  такая, что limn→∞ξ1n=∞ ,limn→∞f(ξ1n)=∞ (1.1). Зафиксируем точки ξi∈[xi−1,xi],i=2,k, тогда сумма ∑ki=2f(ξi)Δxiбудет иметь вполне определенное значение, поэтому в силу (1.1): limn→∞στ(f,ξ,1...,ξ)k=limn→∞(f(ξ1n)Δx1+∑ki=2f(ξi)Δxi)=∞ и значит каково бы ни было М>0 всегда можно подобрать номер n0, что если на первом отрезке [x0,x1] взять точку ξ1n0получим: ∣ ∣  στ(f,ξ1n0,ξ2,...,ξk)∣ ∣  >M, => суммы στ не могут стремиться к конечному пределу при мелкости разбиения δτ=∣τ∣→0 . Действительно, если бы существовал конечный предел lim∣τ∣→0στ=A, то для любого ε>0 нашлось бы такое δ(ε)>0, что для разбиения τ={xi}i=ki=0 отрезка [a,b] мелкости ∣τ∣<δ(ε)  при любом выборе точек ξi∈[xi−1,xi],i=1,k, ∣στ−A∣<ε  и =>∣στ∣=∣(στ−A)+A∣≤∣στ−A∣+∣A∣<ε+∣A∣ . В случае  неограниченности функции f для любого разбиения τ (в т.ч. и для такого, что∣τ∣<δ(ε))  при  любом фиксированном ε>0 можно так выбрать ξi, что выполняется неравенство ∣στ∣>∣A∣+ε . Это противоречие доказывает теорему. Ч.и.т.д. Условие ограниченности функции f необходимое, но НЕ является достаточным. Например, для функции Дирихле: D(x) на [0,1]. Она ограничена, но не интегрируема, т.к. для любого разбиения интегрируемые суммы στ стремятся к 1 если выбрать ξi  рациональными, и к 0 если иррациональными, то есть не стремятся ни к какому пределу.                                                           

16.3 Критерий Дарбу для одномерного интеграла.

Пусть вещественнозначная функция   определена и ограничена на отрезке  . Пусть   и   - верхний и нижний интегралы Дарбу функции   на заданном отрезке соответственно. Тогда следующие 3 условия эквивалентны:

•  интегрируема по Риману на отрезке  ,

• ,

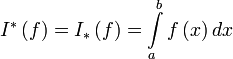, где   и   — некоторое разбиение и его мелкость.

17 Первая теорема о среднем для одномерного интеграла.

18.1 Интеграл как функция верхнего предела.

18 Формула Ньютона-Лейбница.

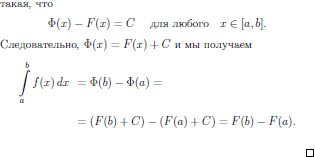
19.1 Длина спрямляемой кривой.

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных. Для наглядности рассмотрим трёхмерное пространство. Пусть непрерывная кривая   задана параметрически:

,

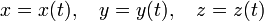(1)

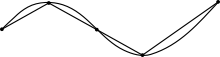
Приближение кривой ломаными

где  . Рассмотрим всевозможные разбиения интервала значений параметра   на   отрезков:  . Соединив точки кривой   отрезками прямых, мы получим ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных.

Всякая непрерывная кривая имеет длину, конечную или бесконечную. Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна. В математическом анализе выводится формула для вычисления длины   отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

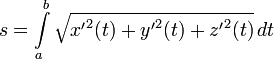
(2)

Формула подразумевает, что   и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

.

19.2 Площадь квадрируемой области.

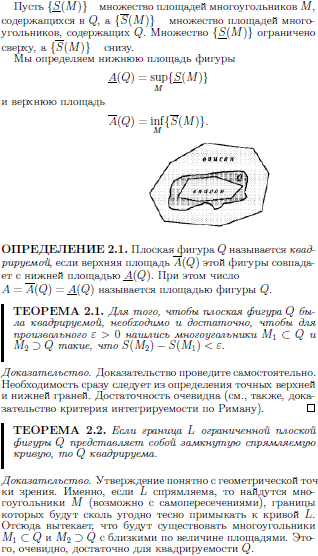
19.3 Объем тел вращения, площадь поверхности.

20.1 Непрерывность отображений.

Непрерывное отображение или непрерывная функция в математике — это отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений.

Наиболее общее определение формулируется для отображений топологических пространств: непрерывным считается отображение, при котором прообраз всякого открытого множества открыт. Непрерывность отображений других типов пространств — метрических, нормированных и т. п. пространств — является непосредственным следствием общего (топологического) определения, но формулируется с использованием структур, заданных в соответствующих пространствах — метрики, нормы и т. д.

В математическом анализе и комплексном анализе, где рассматриваются числовые функции и их обобщения на случай многомерных пространств, непрерывность функции вводится на языке пределов: такие определения непрерывности были исторически первыми и послужили основой для формирования общего понятия.

Существование непрерывных отображений между пространствами, позволяет «переносить» свойства одного пространства в другое: например, непрерывный образ компактного пространства также является компактным.

Непрерывное отображение, которое обладает обратным и также непрерывным отображением, называется гомеоморфизмом. Гомеоморфизм порождает на классе топологических пространств отношение эквивалентности; пространства, гомеоморфные друг другу, обладают одними и теми же топологическими свойствами, а сами свойства, которые сохраняются при гомеоморфизмах, называются топологическими инвариантами.