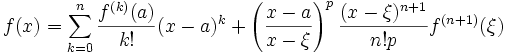- •2.3 Арифметические свойства.
- •Доказательство:
- •Свойства
- •6.4 Ограниченность функции в окрестности точки непрерывности.
- •7.1 Теорема Вейерштрасса о гранях непрерывной функции.
- •Доказательство для r
- •7.2 Теорема Больцано-Коши о промежуточных значениях.
- •Доказательство
- •Различные формы остаточного члена
- •16.2 Необходимое условие интегрируемости функции одной переменной.
- •20.2 Свойства непрерывных отображений
- •21.3 Цепное правило дифференцируемости суперпозиции.
- •Связь с градиентом
- •23.2 Условный экстремум.
- •Условный экстремум. Метод Лагранжа.
- •Метод множителей Лагранжа
- •Алгоритм исследования функции двух переменных на условный экстремум
- •Пример №1
- •25.1 Ядра Дирихле.
6.4 Ограниченность функции в окрестности точки непрерывности.
Локальные
Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
Если функция
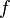 непрерывна
в точке
и
непрерывна
в точке
и 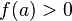 (или
(или  ),
то
),
то  (или
(или 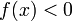 )
для всех
)
для всех  ,
достаточно близких к
.
,
достаточно близких к
.Если функции и
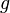 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции  и
и 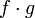 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
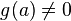 ,
то функция
,
то функция 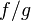 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
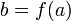 ,
то их композиция
,
то их композиция 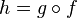 непрерывна
в точке
.
непрерывна
в точке
.
Глобальные
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
Областью значений функции , непрерывной на отрезке
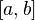 ,
является отрезок
,
является отрезок 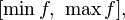 где
минимум и максимум берутся по отрезку
.
где
минимум и максимум берутся по отрезку
.Если функция непрерывна на отрезке и
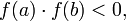 то
существует точка
то
существует точка 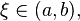 в
которой
в
которой 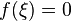 .
.Если функция непрерывна на отрезке и число
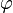 удовлетворяет
неравенству
удовлетворяет
неравенству 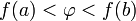 или
неравенству
или
неравенству 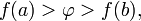 то
существует точка
в
которой
то
существует точка
в
которой 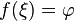 .
.Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
 и
и 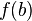 .
.Если функции и непрерывны на отрезке , причем
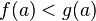 и
и 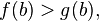 то
существует точка
в
которой
то
существует точка
в
которой 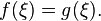 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную точку.
7.1 Теорема Вейерштрасса о гранях непрерывной функции.
Пусть
дана непрерывная числовая функция,
определённая на отрезке, то есть ![]() и
и ![]() .
Пусть
.
Пусть
![]()
— точные
верхняя и нижняя
границы множества значений функции
соответственно.
Тогда эти значения конечны (![]() )
и достигаются (существуют
)
и достигаются (существуют ![]() такие,
что
такие,
что ![]() ).
).
Доказательство для r
Пусть ![]() —
функция, отвечающая условиям теоремы
(на компакте
),
—
функция, отвечающая условиям теоремы
(на компакте
), ![]() .
Возьмём последовательность чисел
.
Возьмём последовательность чисел ![]() таких,
что
таких,
что ![]() и
и ![]() .
Для каждого
.
Для каждого ![]() найдётся
точка
найдётся
точка ![]() ,
такая что
,
такая что ![]() .
Имеем дело с компактом, поэтому,
согласно теореме Больцано —
Вейерштрасса из последовательности
можно
выделить сходящуюся последовательность
.
Имеем дело с компактом, поэтому,
согласно теореме Больцано —
Вейерштрасса из последовательности
можно
выделить сходящуюся последовательность ![]() ,
предел которой лежит в
.
,
предел которой лежит в
.
Для
любого
справедливо ![]() ,
поэтому, применяя предельный переход,
получаем
,
поэтому, применяя предельный переход,
получаем ![]() и
в силу непрерывности функции существует
точка
и
в силу непрерывности функции существует
точка ![]() такая,
что
такая,
что ![]() и,
следовательно
и,
следовательно ![]() .
.
Таким образом
функция
ограничена
и достигает своей верхней грани при ![]() .
Аналогично и для нижней грани.
.
Аналогично и для нижней грани.
7.2 Теорема Больцано-Коши о промежуточных значениях.
Пусть
дана непрерывная функция на отрезке ![]() Пусть
также
Пусть
также ![]() и
без ограничения общности предположим,
что
и
без ограничения общности предположим,
что ![]() Тогда
для любого
Тогда
для любого ![]() существует
существует ![]() такое,
что
такое,
что ![]() .
.
Доказательство
Рассмотрим
функцию ![]() Она
непрерывна на отрезке
и
Она
непрерывна на отрезке
и ![]() ,
, ![]() Покажем,
что существует такая точка
Покажем,
что существует такая точка ![]() ,
что
,
что ![]() Разделим
отрезок
точкой
Разделим
отрезок
точкой ![]() на
два равных по длине отрезка, тогда
либо
на
два равных по длине отрезка, тогда
либо ![]() и
нужная точка
и
нужная точка ![]() найдена,
либо
найдена,
либо ![]() и
тогда на концах одного из полученных
промежутков функция
и
тогда на концах одного из полученных
промежутков функция ![]() принимает
значения разных знаков (на левом конце
меньше нуля, на правом больше).
принимает
значения разных знаков (на левом конце
меньше нуля, на правом больше).
Обозначив
полученный отрезок ![]() ,
разделим его снова на два равных по
длине отрезка и т.д. Тогда, либо через
конечное число шагов придем к искомой
точке
,
либо получим последовательность вложенных
отрезков
,
разделим его снова на два равных по
длине отрезка и т.д. Тогда, либо через
конечное число шагов придем к искомой
точке
,
либо получим последовательность вложенных
отрезков ![]() по
длине стремящихся к нулю и таких, что
по
длине стремящихся к нулю и таких, что
![]()
Пусть
-
общая точка всех отрезков
, ![]() Тогда
Тогда ![]() и
в силу непрерывности функции
и
в силу непрерывности функции ![]()
![]()
Поскольку
![]()
получим, что
7.3 Теорема Кантора о равномерной непрерывности.
![]()

8.1 Дифференцируемость, таблица производных.
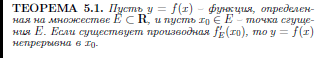


8.2 Производная сложной функции.

8.3 Дифференцируемость обратной функции.
Теорема.
Пусть функция ![]() является обратной для функции
является обратной для функции ![]() .
Если существует отличная от нуля
производная функции
по переменной x, то существует и
производная обратной функции
по переменной y. При этом
.
Если существует отличная от нуля
производная функции
по переменной x, то существует и
производная обратной функции
по переменной y. При этом
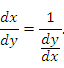
Доказательство. По определению производной
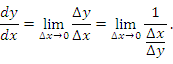
Согласно
теореме о непрерывности дифференцируемых
функциях, ![]() является непрерывной функцией и,
следовательно,
является непрерывной функцией и,
следовательно, ![]() при
∆x → 0. Тогда
при
∆x → 0. Тогда
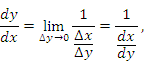
что влечет за собой доказываемое утверждение.

8.4 Знак производной и монотонность функции.
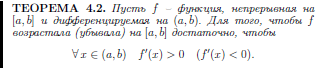
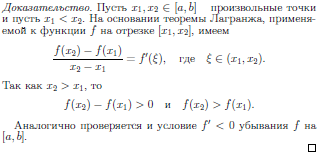
9 Теорема Ферма о производной в точке экстремума.
Пусть функция ![]() имеет
во внутренней точке области
определения
имеет
во внутренней точке области
определения ![]() локальный
экстремум. Пусть также существуют односторонние
производные
локальный
экстремум. Пусть также существуют односторонние
производные ![]() конечные
или бесконечные. Тогда
конечные
или бесконечные. Тогда
если — точка локального максимума, то
![]()
если — точка локального минимума, то
![]()
В частности, если функция имеет в производную, то
![]()
Доказательство
Предположим,
что ![]() .
Тогда
.
Тогда ![]() .
.
Поэтому:
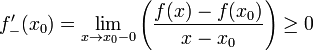 ,
,
 .
.
Если
производная ![]() определена,
то получаем
определена,
то получаем
![]() ,
,
то есть ![]()
10 Теорема Ролля о нуле производной.
Теорема Ро́лля (теорема о нуле производной) утверждает, что
Если вещественная функция, непрерывная на
отрезке |
Доказательство
Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.

![]()
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
Следствие
Если непрерывная функция
обращается в ноль в
различных
точках, то ее производная обращается в
ноль по крайней мере в ![]() различных
точках, причем эти нули производной
лежат в выпуклой оболочке нулей исходной
функции. Это следствие легко проверяется
для случая действительных корней, однако
имеет место и в комплексном случае.
различных
точках, причем эти нули производной
лежат в выпуклой оболочке нулей исходной
функции. Это следствие легко проверяется
для случая действительных корней, однако
имеет место и в комплексном случае.
11.1 Теорема Коши о среднем.

11.2 теорема Лагранжа о среднем.


12 Теорема Дарбу о свойстве производной.

13.1 Формула Тейлора с общим остатком.
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции вокрестности некоторой точки.
Теорема:
тогда:
|
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).