- •2.3 Арифметические свойства.
- •Доказательство:
- •Свойства
- •6.4 Ограниченность функции в окрестности точки непрерывности.
- •7.1 Теорема Вейерштрасса о гранях непрерывной функции.
- •Доказательство для r
- •7.2 Теорема Больцано-Коши о промежуточных значениях.
- •Доказательство
- •Различные формы остаточного члена
- •16.2 Необходимое условие интегрируемости функции одной переменной.
- •20.2 Свойства непрерывных отображений
- •21.3 Цепное правило дифференцируемости суперпозиции.
- •Связь с градиентом
- •23.2 Условный экстремум.
- •Условный экстремум. Метод Лагранжа.
- •Метод множителей Лагранжа
- •Алгоритм исследования функции двух переменных на условный экстремум
- •Пример №1
- •25.1 Ядра Дирихле.
Свойства
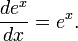 Данное
свойство играет важную роль в решении
дифференциальных уравнений. Так,
например, единственным решением
дифференциального уравнения
Данное
свойство играет важную роль в решении
дифференциальных уравнений. Так,
например, единственным решением
дифференциального уравнения 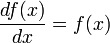 является
функция
является
функция 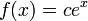 ,
где c — произвольная константа.
,
где c — произвольная константа.Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
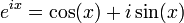
предел
![]()
Для любого комплексного числа z верны следующие равенства:
![]()
3.3 Число e.



4.1 Числовые ряды.
Пусть ![]() — числовая
последовательность; рассмотрим наравне
с данной последовательностью
последовательность
— числовая
последовательность; рассмотрим наравне
с данной последовательностью
последовательность
![]()
каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида
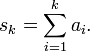
Вообще, для обозначения ряда используется символ
![]()
поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.
В соответствии с этим говорится о сходимости числового ряда:
числовой ряд сходится, если сходится последовательность его частичных сумм;
числовой ряд расходится, если расходится последовательность его частичных сумм:
числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Если числовой ряд сходится, то
предел ![]() последовательности
его частичных сумм носит название суммы
ряда:
последовательности
его частичных сумм носит название суммы
ряда:
![]()
Операции над рядами
Пусть заданы сходящиеся ряды ![]() и
и ![]() .
Тогда:
.
Тогда:
Их суммой называется ряд
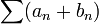
Их произведением по Коши называется ряд
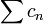 ,
где
,
где 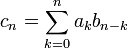
Если оба ряда сходятся, то их сумма сходится, если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.
Критерий абсолютной сходимости
Числовой (действительный или комплексный)
ряд ![]() называется
абсолютно сходящимся, если сходится
ряд
называется
абсолютно сходящимся, если сходится
ряд ![]() .
.
Ряд ![]() сходится
абсолютно тогда и только тогда, когда
сходятся оба положительных ряда
сходится
абсолютно тогда и только тогда, когда
сходятся оба положительных ряда ![]() и
и ![]() Где
Где ![]()

Доказательство. Если
сходится ![]() то
по признаку сравнения тем более
сходятся
и
Наоборот,
если сходятся
и
то
по признаку сравнения тем более
сходятся
и
Наоборот,
если сходятся
и ![]() то
сходится и их сумма
то
сходится и их сумма ![]()
4.2 Признак сравнения для рядов.
Пусть даны два знакоположительных ряда:
.
Тогда, если, начиная с некоторого места
(
то из сходимости ряда следует сходимость . Или же, если ряд расходится, то расходится и .
|
Доказательство
Обозначим ![]() частные
суммы ряда
частные
суммы ряда ![]() .
Из неравенств
.
Из неравенств ![]() следует,
что
следует,
что ![]() Поэтому
из ограниченности
Поэтому
из ограниченности ![]() вытекает
ограниченность
вытекает
ограниченность ![]() а
из неограниченности
а
из неограниченности ![]() следует
неограниченность
следует
неограниченность ![]() Справедливость
признака вытекает из критерия сходимости
для
Справедливость
признака вытекает из критерия сходимости
для ![]()
4.3 Признак Коши сходимости рядов.
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
с
неотрицательными членами существует
такое число |
Предельная форма
Условие радикального признака равносильно следующему:
![]()
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
-
Если для ряда
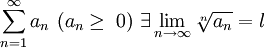 ,
то
,
тоесли
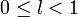 ряд
сходится,
ряд
сходится,если
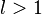 ряд
расходится,
ряд
расходится,если
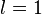 вопрос
о сходимости ряда остается открытым.
вопрос
о сходимости ряда остается открытым.
Доказательство
1. Пусть ![]() .
Очевидно, что существует такое
,
что
.
Очевидно, что существует такое
,
что ![]() .
Поскольку существует предел
.
Поскольку существует предел ![]() ,
то подставив в определение предела
выбранное
получим:
,
то подставив в определение предела
выбранное
получим:
![]()
Раскрыв модуль, получаем:
![]()
![]()
![]()
Поскольку
,
то ряд ![]() сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
2. Пусть
.
Очевидно, что существует такое
,
что ![]() .
Поскольку существует предел
,
то подставив в определение предела
выбранное
получим:
.
Поскольку существует предел
,
то подставив в определение предела
выбранное
получим:
Раскрыв модуль, получаем:
Поскольку
,
то ряд ![]() расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
4.4 Признак Даламбера сходимости рядов.
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
существует такое число ![]() ,
, ![]() ,
что начиная с некоторого номера
выполняется неравенство
,
что начиная с некоторого номера
выполняется неравенство
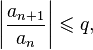
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
![]()
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме
Если существует предел
![]()
то рассматриваемый ряд абсолютно
сходится если ![]() ,
а если
,
а если ![]() —
расходится.
—
расходится.
Замечание. Если ![]() ,
то признак д′Аламбера не даёт ответа
на вопрос о сходимости ряда.
,
то признак д′Аламбера не даёт ответа
на вопрос о сходимости ряда.
Доказательство
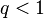 ,
тогда существует
,
тогда существует 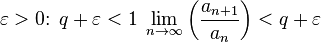 ,
существует
,
существует 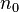 ,
для любого
,
для любого 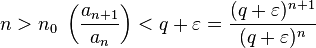 .
Ряд
из
.
Ряд
из 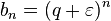 сходится
(как геометрическая прогрессия). Значит,
ряд из
сходится
(как геометрическая прогрессия). Значит,
ряд из 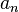 сходится
(по признаку сравнения).
сходится
(по признаку сравнения).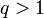 ,
тогда существует
,
тогда существует 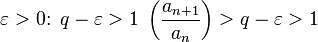 .
. 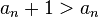 для
любого
для
любого  .
Тогда
не
стремится к нулю и ряд расходится.
.
Тогда
не
стремится к нулю и ряд расходится.
4.1 Эквивалентность двух определений предела функции.
Теорема. Определения предела функции по Коши и по Гейне эквивалентны.
В определениях предела функции f(x) по
Коши и по Гейне предполагается, что
функция f определена в некоторой
проколотой окрестности точки ![]() ,
т.е. существует число
,
т.е. существует число![]() такое,
что
такое,
что ![]() .
.
а) Пусть число А есть предел функции f в
точке
по
Коши; тогда![]() и
и
![]()
![]() (A).
(1)
(A).
(1)
Рассмотрим произвольную последовательность ![]() ,
сходящуюся к числу
и
такую, что
,
сходящуюся к числу
и
такую, что ![]() для
всех
для
всех ![]() ,
N-натуральные числа. Согласно определению
предела последовательности для найденного
в (1) числа
,
N-натуральные числа. Согласно определению
предела последовательности для найденного
в (1) числа ![]() можно
указать номер
можно
указать номер ![]() такой,
что
такой,
что ![]() ,
откуда в силу условия (1) следует, что
,
откуда в силу условия (1) следует, что ![]() .
Таким образом,
(A),
(2), где
.
Таким образом,
(A),
(2), где ![]() ,
причем усл-е (2) выполняется для любой
посл-ти {Xn}
,
причем усл-е (2) выполняется для любой
посл-ти {Xn}
такой, что ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() ,
т.е. число А – предел функции f(x) в
точке
по
Гейне.
,
т.е. число А – предел функции f(x) в
точке
по
Гейне.
б) Докажем, что если число А есть предел
функции f(x) в точке
по
Гейне, то это же число является пределом
функции f по Коши, т.е. выполняется условие
(1). Допустим, что это неверно. Тогда
![]()
![]() .
(3)
.
(3)
Согласно (3) в качестве ![]() можно
взять любое число из полуинтервала
можно
взять любое число из полуинтервала ![]() .
Возьмем
.
Возьмем![]() ,
где
,
N-натуральные числа, и обозначим
,
где
,
N-натуральные числа, и обозначим ![]() .
Тогда в силу (3) для любого
,
N-натуральные числа, выполняются
неравенства
.
Тогда в силу (3) для любого
,
N-натуральные числа, выполняются
неравенства
![]() ,
(4)
,
(4)
![]() .
(5)
.
(5)
Из (4) следует, что ![]() и
и ![]() при
всех
,
а из (5) заключаем, что число А не может
быть пределом последовательности
при
всех
,
а из (5) заключаем, что число А не может
быть пределом последовательности ![]() .
Следовательно, число А не является
пределом функции f в точке
по
Гейне. Полученное противоречие доказывает,
что должно выполняться утверждение
(1).
.
Следовательно, число А не является
пределом функции f в точке
по
Гейне. Полученное противоречие доказывает,
что должно выполняться утверждение
(1).
5.2 Свойства предела функции, критерий Коши.


5.3 Первый замечательный предел
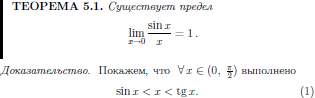


6.1 Непрерывные функции.

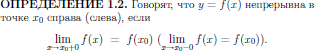



6.2 Односторонние пределы.
Пусть на некотором числовом множестве ![]() задана числовая
функция
задана числовая
функция ![]() и
число
— предельная
точка области определения
и
число
— предельная
точка области определения ![]() .
Существуют различные определения для
односторонних пределов функции
.
Существуют различные определения для
односторонних пределов функции ![]() в
точке
,
но все они эквивалентны.
в
точке
,
но все они эквивалентны.
Односторонний предел по Гейне
Число
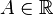 называется правосторонним
пределом (правым пределом, пределом
справа) функции
в
точке
,
если для всякой последовательности
называется правосторонним
пределом (правым пределом, пределом
справа) функции
в
точке
,
если для всякой последовательности 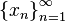 ,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции
,
состоящей из точек, больших числа
,
которая сама сходится к числу
,
соответствующая последовательность
значений функции 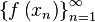 сходится
к числу
сходится
к числу 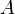 .
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .
![]()
Односторонний предел по Коши
Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число
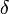 такое,
что для всех
точек
из интервала
такое,
что для всех
точек
из интервала 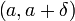 справедливо неравенство
справедливо неравенство 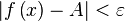 .
.
![]()
Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякого положительного числа отыщется отвечающее ему положительное число , такое, что для всех точек из интервала
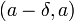 справедливо
неравенство
.
справедливо
неравенство
.
![]()
Односторонний предел как предел вдоль фильтра
Пусть ![]() и
и ![]() Тогда
системы множеств
Тогда
системы множеств
![]()
и
![]()
являются фильтрами. Пределы вдоль этих фильтров совпадают с соответствующими односторонними пределами:
![]()
![]()
Обозначения
Правосторонний предел принято обозначать любым из нижеследующих способов:
![]()
Аналогичным образом для левосторонних пределов приняты обозначения:
![]()
При этом используются также сокращённые обозначения:
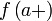 и
и 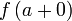 для
правого предела;
для
правого предела;
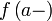 и
и 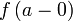 для
левого предела.
для
левого предела.
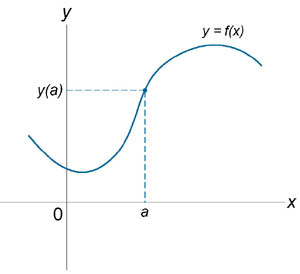
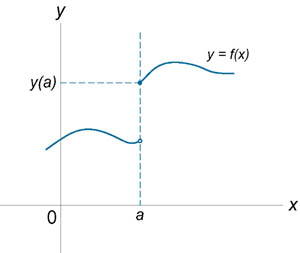
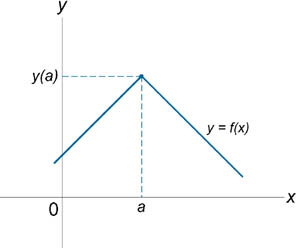
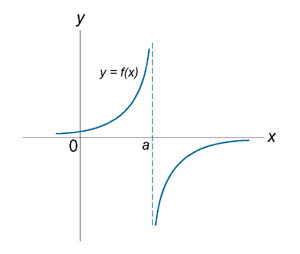
6.3 Классификация точек разрыва. Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая точка
называется точкой конечного
разрыва. Модуль разности значений
односторонних пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. |
|||||||||||||||