1. Аксиомы действительных чисел.

Множество R = {x, y, z,…} действительных чисел - множество мощности континуум, на котором определены две операции (сложение и умножение) и отношение упорядоченности (x ≤ y), удовлетворяющие аксиомам

I.1.x + y = y + x;

I.2.(x + y) + z = x + (y + z);

I.3. Существует такой элемент 0∈R, что 0 + х = х для ∀х∈R;

I.4. Для каждого элемента х∈R существует такой элемент -х, что х + (-х) = 0;

II.1. x·y = y·x;

II.2. (x·y)·z = x·(y·z);

II.3. Существует такой элемент 1∈R, что 1·х = х для ∀х∈R;

II.4. Для каждого элемента х∈R существует такой элемент х-1, что х·х-1 = 1;

III.1. x·(y + z) = x·y + x·z;

IV.1. Отношение {(x ≤ y)∧(y ≤ x)} эквивалентно отношению x = y;

IV.2. Для любых двух элементов х∈R, y∈R или х ≤ у, или y ≤ x;

IV.3. Из x ≤ y и y ≤ z следует x ≤ z;

IV.4. Из x ≤ y следует x + z ≤ y + z для любых x, y, z ∈ R;

IV.5. Из 0 ≤ x и 0 ≤ y следует 0 ≤ x·y;

Отношение x ≤ y записывается также в форме y ≥ x. Отношение {(x ≤ y)∧(x ≠ y)} записывается в форме х < у.

V. Аксиома непрерывности: для любых элементов х ∈ R, y ∈ R таких, что х < у, существует элемент z ∈ R, такой что х < z < у.

VI. Аксиома Архимеда: для любых элементов х ∈ R, y ∈ R таких, что 0 < х, 0 < у, существует такое натуральное число n, что у ≤ n·х;

VII. Аксиома о вложенных отрезках: если {[an, bn]} - счётная последовательность отрезков, таких что an ≤ an+1 и bn+1 ≤ bn, при ∀n, то пересечение этой последовательности непусто, т.е. ∃ х ∈ R: х∈[an, bn] для ∀n.

2. Грани числовых множеств.

Определения:

Если , то A называется ограниченным сверху множеством.

называется верхней границей множества А.

Если , то A называется ограниченным снизу множеством.

называется нижней границей множества А.

Если , то A называется ограниченным множеством.

Если A — ограничено сверху, то наимешьшая из его верхних границ называется верхней гранью.

b = supA ("супремум")

Если A — ограничено снизу, то наибольшая из его нижних границ называется нижней гранью.

b = infA ("инфимум")

Существование грани множества

Теорема:

Если А ограничено сверху, то у него существует верхняя грань (аналогично для А, ограниченного снизу).

Пусть M — множество верхних границ А. Так как А ограничено сверху, то  . По определению верхней границы:  . По аксиоме непрерывности: : .  — наименьшая из верхних границ А. Получили, что d — верхняя граница А, и d не больше всех верхних границ А  . Аналогично для нижней грани ограниченного снизу множества А.

1.3 Лемма о вложенных отрезках

Для всякой системы вложенных отрезков

существует хотя бы одна точка  , принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю:

то   — единственная общая точка всех отрезков данной системы.

Отрезки в формулировке теоремы нельзя заменить на открытые интервалы. Например,

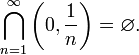
Доказательство 

1) Существование общей точки. Множество левых концов отрезков   лежит на числовой прямой левее множества правых концов отрезков  , поскольку

В силу аксиомы непрерывности, существует точка  , разделяющая эти два множества, то есть

в частности

Последнее неравенство означает, что   — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки   и  , принадлежащие всем отрезкам системы:

Тогда для всех номеров   выполняются неравенства:

В силу условия стремления к нулю длин отрезков для любого   для всех номеров  , начиная с некоторого будет выполняться неравенство

Взяв в этом неравенстве  , получим

Противоречие. Лемма доказана полностью.

1.4

Непрерывность функции   на отрезке   означает, что для всякой точки   отрезка   и произвольного   найдется такая окрестность   точки  , в которой любые два значения функции отличаются не более чем на  :

Фиксируем   и для каждой точки   отрезка   выберем указанную окрестность   (для каждого   будет свое  ). Полученная система интервалов образует открытое покрытие отрезка, из которого согласно лемме Гейне — Бореля мы выберем конечное подпокрытие  . Нетрудно видеть, что можно подобрать такое  , что всякий отрезок длины   целиком содержится в одном из интервалов покрытия  . Отсюда следует, что если   отличаются не более чем на  , то они содержатся в одном и том же интервале покрытия, а значит, значения функции в этих точках отличаются не более чем на  .

Тем самым для произвольно взятого   найдено  , такое что

Это и означает, что функция   равномерно непрерывна на отрезке  .

2.1-2 Предел последовательности. Обязательное условие сходимости.

Число   называется пределом числовой последовательности  , если последовательность   является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

Предел последовательности.

Пусть дано топологическое пространство   и последовательность  Тогда, если существует элемент   такой, что

,

где   — открытое множество, содержащее  , то он называется пределом последовательности  . Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент   такой, что

,

где   — метрика, то   называется пределом  .

2.3 Арифметические свойства.

• Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.

  • Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.

• Однородность. Константу можно выносить из-под знака предела.

• Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

• Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.

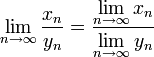
2.4 Предельный переход в неравенствах.

Теорема о предельном переходе в неравенстве.  Пусть  \\  тогда

Доказательство. (от противного)

Пусть  .

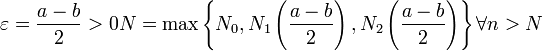
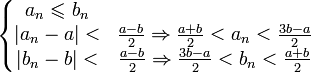
 - противоречие.

3.1 Критерий Коши сходимости последовательности

Из определения сходимости последовательности   к точке a вытекает, что для любого   интервалом длиной 2  можно накрыть всю эту последовательность, исключением может быть конечное число ее элементов, если середину интервала поместить в точке  . Справедливо и обратное : если последовательность   такова, что для любого  можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, поместив центр интервала в некоторую точку, то она сходится. Сформулируем это утверждение более точно.

Определение. Подпоследовательность    называется последовательностью Коши или фундаментальной, если 

Теорема ( Критерий Коши ). Для того, чтобы последовательность  сходилась, необходимо и достаточно чтобы она была фундаментальной.

Доказательство:

Необходимость. Пусть   сходится. 

Достаточность. Пусть   - фундаментальная последовательность. Докажем, что она ограничена и  .

Так как последовательность фундаментальна, то  , в  -окресности которой существуют все элементы  .

Предположим,   .

В отрезке [A, -A] содержатся все элементы последовательности, т.е.   - ограничена.

Вследствие теоремы Больцано-Вейерштрасса ( ) < ( ).

 в силу произвольности 

3.2 Свойства монотонных последовательностей

1. Пусть {a } – возрастающая (убывающая) последовательность, С – некоторое число. Тогда а) {a +С} – возрастающая (убывающая) последовательность; б) {Сa } – возрастающая (убывающая) последовательность при С>0; в) {Сa } – убывающая (возрастающая) последовательность при С<0. 2. Если одна из последовательностей {a } и {b } возрастающая, а другая неубывающая, то{a +b } – возрастающая последовательность; если же одна из этих последовательностей убывающая, а другая невозрастающая, то {a +b } – убывающая последовательность. 3.а) Если одна из последовательностей {a } и {b } возрастающая, а другая неубывающая, то {a b } – возрастающая последовательность при a >0, b >0 для любых n N и {a b } – убывающая последовательность при a <0, b <0 для любых n N; б) если одна из последовательностей {a } и {b } убывающая, а другая невозрастающая, то {a b } – убывающая последовательность при a >0, b >0 для любых n N и {a b } – возрастающая последовательность при a <0, b <0 для любых n N. 4. Если {a } – возрастающая (убывающая) последовательность, то а) { } – убывающая (возрастающая) последовательность при a >0 для любых n N; б) { } – возрастающая (убывающая) последовательность при a <0 для любых n N. 5. Если все члены последовательности {a } принадлежат множеству M, которое содержится в области определения функции у=f(x), то а) если {a } – возрастающая (убывающая) последовательность и функция у=f(x)возрастающая на множестве М, то {f(a )} – возрастающая (убывающая) последовательность; б) если { } – возрастающая (убывающая) последовательность и функция у=f(x)убывающая на множестве М, то {f(a )} – убывающая (возрастающая) последовательность. Например, из свойства 5 следует, что последовательности a = , b =lnn, с =n  являются возрастающими, а последовательности a = , b =ln  , с =( ) являются убывающими.

3.2.2 Свойства 2

• Ограниченность.

  • Всякая неубывающая последовательность ограничена снизу.

  • Всякая невозрастающая последовательность ограничена сверху.

  • Всякая монотонная последовательность ограничена по крайней мере с одной стороны.

• Монотонная последовательность сходится тогда и только тогда, когда она ограничена с обеих сторон.(Теорема Вейерштрасса об ограниченных монотонных последовательностях)

  • Сходящаяся неубывающая последовательность ограничена сверху своим пределом.

  • Сходящаяся невозрастающая последовательность ограничена снизу своим пределом.

3.3 Число е.

Это математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e». Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Число e может быть определено несколькими способами.

• Через предел:

 (второй замечательный предел).

• Как сумма ряда:

 или  .

• Как единственное число a, для которого выполняется

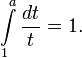
• Как единственное положительное число a, для которого верно