5 Этапы решения нелинейных и трансцендентных уравнений (Подготовка к практическому занятию № 6, 2 часа)

Перед соответствующим практическим занятием по материалам, приведённым в литературных источниках, а также соответствующей лекции, повторите понятия корня уравнения, изолированного, простого и кратного корней; этапы решения нелинейных и трансцендентных уравнений, графический метод нахождения корней уравнения, их уточнение; метод половинного деления, его скорость сходимости; критерии окончания процесса вычисления корня, окончания процесса и количество требуемых итераций.

Рассмотрим решение типичных задач на указанную тему.

№ 1. Отделить корни графически и уточнить один из них методом проб с точностью до 0,01:

Решение. Переписываем уравнение в виде Обозначим построим графики функций (рисунок 1).

Рисунок 1 – Графики функций

Очевидно, что уравнение имеет один корень х₁ = –0,8.

Чтобы уточнить корень методом проб, выберем промежуток, на концах которого функция имеет разные знаки.

Составим таблицу знаков функции f(x) (таблица 4),

Таблица 4 - Знаки функции f(x)

Для удобства расчётов перейдём к десятичным логарифмам.

Производим вычисления в таблице 5.

Таблица 5 – Вычисление корня функции f(x)

Ответ: х  -0,73.

6 Метод итераций, хорд, метод Ньютона (касательных) (Подготовка к практическому занятию № 7, 2 часа)

Перед соответствующим практическим занятием по материалам, приведённым в литературных источниках, а также соответствующей лекции, повторите понятия и основные факты теории по решению уравнений методами: простой итерации, хорд, Ньютона (касательных), комбинированным; выясните геометрический смысл указанных методов, условия их сходимости, критерий окончания итераций.

Рассмотрим решение типичных задач на указанную тему.

№ 1. Отделить корни аналитически и уточнить один из них методом хорд с точностью до 0,001:

Решение. Отделим корни аналитически. Находим

Составим таблицу знаков функции f(x) (таблица 6):

Таблица 6 – Знаки функции f(x)

Уравнение имеет один действительный корень, лежащий в промежутке [-1,0].

Чтобы уточнить корень, находим вторую производную в промежутке [–1, 0] выполняется неравенство f "(х) < 0.

Для вычислений применяем формулу

где а = –1; х₀ = 0; f(а) = f(–1)= -1-0,2-0,5 + 1,5 = -0,2.

Вычисления располагаем в таблице (таблица 7).

Таблица 7 – Вычисление корня функции f(x)

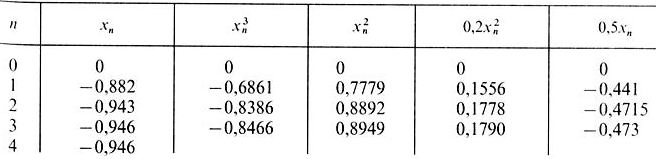
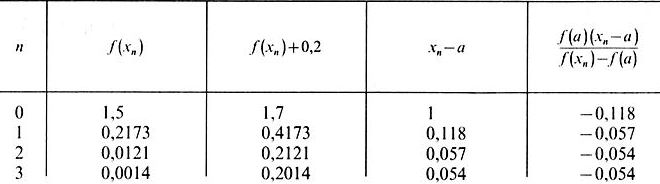
Ответ: х  -0,946.

№ 2. Отделить корни графически и уточнить один из них методом касательных с точностью до 0,001.

.

Решение. Корни для заданной функции уже отделены в метод.указаниях к практическим работам (№ 1) и установили, что он заключен в промежутке [0,6; 0,8]. Уточним этот корень методом касательных. Так как f(0,6) >0, f(0,8) <0, то за начальное приближение примем х_о = 0,8.

Вычисления производим по формуле

Предварительно найдем

Составим таблицу (таблица 8).

Таблица 8 – Итерации для функций

Ответ: х  0,750.

№ 3. Комбинированным методом хорд и касательных решить уравнение третьей степени, вычислив корни с точностью до 0,001.

.

Решение. Корни для заданной функции отделим аналитически.

Составим таблицу знаков функции f(x) (таблица 9).

Таблица 9 – Знаки функции f(x)

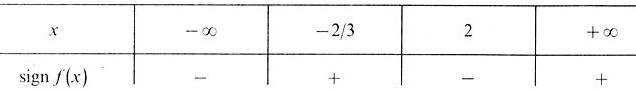
Очевидно, что уравнение имеет три действительных корня:

Уменьшим промежутки, содержащие корни, до 1 (таблица 10).

Таблица 10 – Знаки функции f(x)

Значит,

Уточним один из корней:

При -2  х  -1 имеем f"(x)<0. Для расчётов применим формулы

где и – значения корня соответственно по недостатку и избытку. Полагаем х_о = –2, .

Все вычисления производим в таблице (таблица 11), обозначив

Таблица 11 – Итерации для заданной функции

Ответ: х₁  –1,935.

Замечание. Остальные корни в приведённом выше примере находятся аналогично.

№ 4. Отделив корни уравнения аналитически, уточнить один из них методом итерации с точностью до 0,001.

Решение. Корни для заданной функции отделим аналитически.

Составим таблицу знаков функции (таблица 12).

Таблица 12 – Знаки функции f(x)

Очевидно, что уравнение имеет единственный корень, лежащий в промежутке [-1, 0]. Приведём уравнение к виду х = (х) так, чтобы при -1  х  0. Т.к. то можно взять k = 10. Тогда

Пусть х_о = 0, тогда х_n+1 = (х_n). Вычисления располагаем в таблице (таблица 13).

Таблица 13 – Итерации для заданной функции

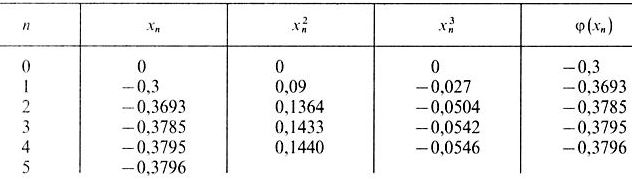
Ответ: х  -0,38.