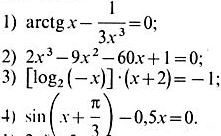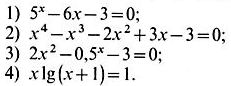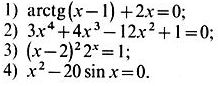Этапы решения нелинейных и трансцендентных уравнений

(Практическое занятие № 5, 2 часа)

План занятия:

1. Отделение корней нелинейных и трансцендентных уравнений;

2. Локализация корней;

3. Решение задач методом половинного деления.

Ход занятия:

Вопросы к студентам:

1) напомните понятия корня уравнения, изолированного корня;

2) перечислите этапы решения нелинейных и трансцендентных уравнений;

3) в чём заключается графический метод нахождения корней уравнения;

4) в чём заключается процесс уточнения приближенных корней;

5) сформулируйте понятия простого и кратного корней;

6) в чём заключается метод половинного деления;

7) поясните какова скорость сходимости;

8) поясните каков критерии окончания процесса вычисления корня;

9) приведите рассуждения по поводу окончания процесса и количество требуемых итераций.

Рассмотрим решение типичных задач на указанную тему.

№ 1. Отделить корни аналитически и уточнить один из них методом проб с точностью до 0,01:

Решение.

Полагая f(x) = x⁴ – х³ – 2х² + 3х – 3, имеем f '(x) = 4x³ – 3х² – 4х + 3. Найдем корни производной:

Составим таблицу знаков функции f(x) (таблица 4).

Таблица 4 – Знаки функции f(x)

Из таблицы видно, что уравнение имеет два действительных корня:

Уменьшим промежутки, в которых находятся корни (таблица 5).

Таблица 5 – Знаки функции f(x) после уточнения

Следовательно,

Уточним один из корней, например методом проб до сотых долей. Все вычисления удобно производить, используя следующую таблицу (таблица 6 на следующей странице).

Таблица 6 – Вычисление методом проб

Ответ:

В метод.указаниях по самостоятельней работе приведено решение примера на графическое отделение корней.

Самостоятельно решаем по вариантам задания.

Задание № 1.

1) Отделить корни аналитически.

2) Отделить корни аналитически и уточнить один из них методом проб с точностью до 0,01.

3) Отделить корни графически.

4) Отделить корни графически и уточнить один из них методом проб с точностью до 0,01.

Вариант № 1	Вариант № 2	Вариант № 3
Вариант № 4	Вариант № 5	Вариант № 6
Вариант № 7	Вариант № 8	Вариант № 9
Вариант № 10	Вариант № 11	Вариант № 12
Вариант № 13	Вариант № 14	Вариант № 15

Материалы лекции

Тема 3 Методы решения нелинейных и трансцендентных уравнений

6 Этапы решения нелинейных и трансцендентных уравнений

Вопросы лекции: Постановка задачи. Корень уравнения. Простые и кратные корни. Их геометрический смысл. Основные этапы решения: отделение (локализация) корней и итерационное уточнение корней. Отрезок локализации. Способы отделения корней. Метод деления отрезка пополам: итерация метода, скорость сходимости, критерии окончания, количество требуемых итераций.

Постановка задачи

Пусть дано уравнение

f(x) = 0, (6.1)

где функция f(x) определена и непрерывна в конечном или бесконечном интервале a < x < b.

Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ) = 0, называется корнем уравнения (6.1) или нулем функции f(x). Предположим, что уравнение (6.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное нахождение изолированных действительных корней уравнения (6.1) складывается обычно из двух этапов:

1. Отделение корней, то есть установление возможно тесных промежутков [α, β], в которых содержится один и только один корень исходного уравнения (6.1).

2. Уточнение приближенных корней, то есть доведение их до заданной степени точности.

Графическое решение уравнений

Действительные корни уравнения f(x) = 0 приближенно можно определить как абсциссы точек пересечения графика функции y = f(x) с осью ОХ (рисунок 2, а). На практике часто бывает удобнее уравнение (6.1) заменить равносильным ему уравнением

, (6.2)

где функции φ(x) и ψ(x) более простые, чем функция f(x). Тогда, построив графики этих функций, искомые корни получим как абсциссы точек пересечения этих графиков (рисунок 2, б).

а) б)

Рисунок 2 – Графический метод нахождения корней уравнения.

Метод половинного деления (дихотомии)

Сформулируем без доказательства очень важную для рассмотрения дальнейших вопросов теорему.

Теорема: Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [α, β], то есть f(α)·f(β) < 0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x) = 0, а именно: найдётся хотя бы одно число такое, что f(ξ) = 0.

Пусть дано уравнение

f(x) = 0, (6.3)

где функция f(x) определена и непрерывна на интервале [a, b] и f(a)·f(b) < 0. Для нахождения корня уравнения делим отрезок [a, b] пополам:

• если f((a + b)/2) = 0, то ξ = (a + b)/2 является корнем уравнения (6.3);

• если , то выбираем ту половину отрезка [a, (a + b)/2] или [(a + b)/2, b], на концах которого функция f(x) имеет противоположные знаки. Новый суженный отрезок [a₁, b₁] снова делим пополам и проводим тот же анализ и т.д.

Очевидно, что закончить уточнение значения корня можно при достижении условия |а_j – b_j| < ε , где ε > 0 - сколь угодно малое число. Второй способ закончить вычисления - задать максимальное значение невязки: f((a_j + b_j)/2) < ε.

Замечания

• Метод половинного деления очень прост, здесь нет вычислительной формулы и можно обеспечить практически любую точность.

• Как недостаток метода можно отметить его медленную сходимость (за один шаг интервал, где находится корень, сужается всего в два раза).