4.1.2 Расчет конструктивных размеров резисторов

Расчет резистора R9

Номинальное сопротивление резистора 10000 Ом.

Вычисляем коэффициент формы

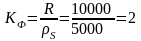
К_ф>1, следовательно, расчет надо начинать с ширины резистора, как с наименьшего размера.

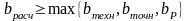(4.4)

где 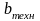– минимальная ширина резистора, определяемая возможностями технологического процесса, ;

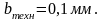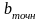– ширина резистора, определяемая точностью изготовления, мм;

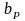– минимальная ширина резистора, определяемая возможностью рассеивания выделяемой мощности, мм.

Определим по формуле:

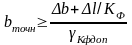(4.5)

где 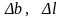– погрешности воспроизведения ширины и длины резистора, зависящие от метода задания конфигурации;

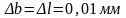
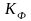– коэффициент формы резистора R1;

– допустимая погрешность коэффициента формы, определенная выше.

Подставляя численные значения в формулу (4.5), получим:

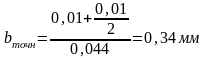
Определим по формуле:

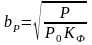(4.6)

где 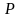– мощность, рассеиваемая резистором R₁ (таблица 4.1);

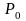– допустимая удельная мощность рассеяния материала,

.

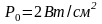Подставляя значения в формулу (4.6), получим:

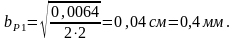
Определяем расчетную ширину резистора исходя из условия (4.4):

.

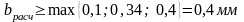Нормиру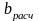ем в соответствии с нормировочным множителем

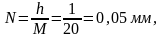
где h=1 мм - шаг координатной сетки и выбран масштаб M 20 : 1

Расчетную длину резистора определяем по формуле:

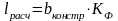(4.7)

По формуле (4.8 ), получи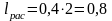м:

мм.

Нормируем полученную величину в соответствии с N:

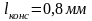
Учтем перекрытия для совмещения пленочных элементов:

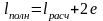(4.8)

где е=0,2мм – размер перекрытия резистора и контактных площадок, зависящий от метода изготовления.

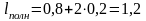мм.

Определяем площадь, занимаемую резистором на подложке:

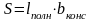(4.9)

Подставив значения в формулу (4.9), получим:

.

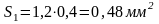Для проверки находят действительную удельную мощность и погрешность резистора. Резистор считается спроектированным правильно, если он удовлетворяет следующим условиям:

• удельная мощность рассеяния 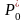не превышает допустимого значения для материала резистора :

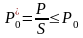(4.10)

• погрешность коэффициента формы 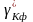не превышает допустимого значения :

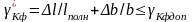(4.11)

• суммарная погрешность не превышает заданной из условий функционирования устройства погрешности :

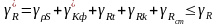. (4.12)

Воспользуемся приведенными выше формулами для проверки резистора R1:

;

;

.

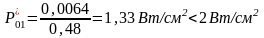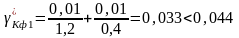Таким образом, условия выполняются, следовательно, резистор R1 спроектирован правильно.

Расчет резисторов R4, R7 – R10 полностью аналогичен расчету резистора R1. Для удобства сведем результаты расчетов в таблицу.

Таблица 4.2.1 – Параметры резисторов R1, R2, R5 – R10

Резистор	R, Ом	Kф	bтехн, мм	bточн, мм	bр, мм	bрасч, мм	lрасч, мм	lконстр, мм	bконстр, мм	lполн, мм	S, мм2
R1	100000	20	0,1	0,34	0,4	0,4	8	8	0,4	8,40	3,36
R2	24000	4,8	0,1	4	0,1	0,28	0,34	0,34	1,4	1,4	1,96
R5	7500	1,5	0,1	0,35	0,5	0,35	0,4	0,41	0,5	0,45	0,225
R6	7500	1,5	0,1	0,35	0,5	0,35	0,4	0,41	0,5	0,45	0,225
R7	7500	1,5	0,1	0,35	0,5	0,35	0,4	0,41	0,5	0,45	0,225
R8	4700	0,94	0,1	0,1	0,45	0,38	0,45	0,46	0,5	0,45	0,225
R9	10000	2	0,1	0,34	0,40	0,40	0,8	0,80	0,40	1,2	0,48
R10	24000	4,8	0,1	4	0,1	0,28	0,34	0,34	1,4	1,4	1,96

Таблица 4.2.2 – Поверочный расчет резисторов R1, R2, R5 – R10

Резистор	P0'<P0, Вт/см2	gКф '<Kф доп, %	gR'<gR, %
R1	1,33	3,33	8,93
R2	1,33	3,33	8,93
R5	0,74	3,33	8,93
R6	0,74	3,33	8,93
R7	0,74	3,33	8,93
R8	1,46	3,41	9,01
R9	1,43	4,10	9,70
R10	1,33	3,33	8,93

Расчет резистора R3

Номинальное сопротивление резистора 1500Ом.

Вычисляем коэффициент формы

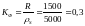
К_ф<1, следовательно расчет надо начинать с длины резистора, как с наименьшего размера.

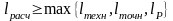(4.13)

где 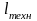– минимальная длина резистора, определяемая возможностями технологического процесса, ;

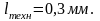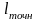– длина резистора, определяемая точностью изготовления, мм;

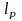– минимальная длина резистора, определяемая возможностью рассеивания выделяемой мощности, мм.

Определим по формуле:

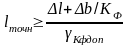(4.14)

где – погрешности воспроизведения ширины и длины резистора, зависящие от метода задания конфигурации;

– коэффициент формы резистора R3;

– допустимая погрешность коэффициента формы, определенная выше.

Подставляя численные значения в формулу (4.14), получим:

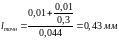
Определим по формуле:

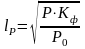(4.15)

где – мощность, рассеиваемая резистором R₂ (таблица 4.1);

– допустимая удельная мощность рассеяния материала,

.

Подставляя значения в формулу (4.15), получим:

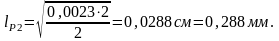
Определяем расчетную ширину резистора исходя из условия (4.13):

.

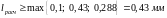Нормируем в соответствии с нормировочным множителем

где h=1 мм - шаг координатной сетки и выбран масштаб M 20 : 1

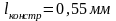
Расчетную ширину резистора определяем по формуле:

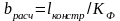(4.16)

По формуле (4.8 ), получи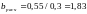м:

мм.

Нормируем полученную величину в соответствии с N:

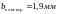
Учтем перекрытия для совмещения пленочных элементов по (4.8),:

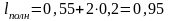мм.

Определяем площадь, занимаемую резистором на подложке по (4.9):

.

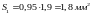Проверим условия (4.10), (4.11) и (4.12)

Воспользуемся приведенными выше формулами для проверки резистора R2:

;

;

.

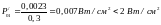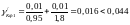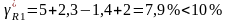Таким образом, условия выполняются, следовательно, резистор R2 спроектирован правильно.

Расчет резисторов R3, R5, R6 полностью аналогичен расчету резистора R2. Для удобства сведем результаты расчетов в таблицу.

Таблица 4.3.1 – Параметры резисторов R3, R4, R11, R12

Резистор	R, Ом	Kф	lтехн, мм	lточн, мм	lр, мм	lрасч, мм	bрасч, мм	lконстр, мм	bконстр, мм	lполн, мм	S, мм2
R3	1500	0,3	0,65	0,3	0,65	0,37	1,83	1,2	1,9	0,95	1,805
R4	1500	0,3	0,65	0,3	0,65	0,37	1,83	1,2	1,9	0,95	1,805
R11	1000	0,2	0,7	0,3	0,7	0,4	1,95	1,2	2	1,15	2,3
R12	1000	0,2	0,7	0,3	0,7	0,4	1,95	1,35	2	1,15	2,3

Таблица 4.3.2 – Поверочный расчет резисторов R2, R3, R5, R6

Резистор	P0'<P0, Вт/см2	gКф '<gKф доп, %	gR'<gR, %
R3	0,30	2,30	7,90
R4	0,30	2,30	7,90
R11	0,10	2,30	7,90
R12	0,10	2,30	7,90