34. Локальный экстремум. Необходимое условие.

Экстре́мум — максимальное или минимальное значение функции на заданном множестве. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Пусть дана функция и— внутренняя точка области определения f. Тогда

x0 называется точкой локального максимума функции f, если существует проколотая окрестность такая, что

x0 называется точкой локального минимума функции f, если существует проколотая окрестность такая, что

Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно.

x0 называется точкой абсолютного (глобального) максимума, если

x0 называется точкой абсолютного минимума, если

Необходимые условия существования локальных экстремумов

Лемма Ферма. Пусть функция дифференцируема в точке локального экстремума x0. Тогда: F '(x0) = 0.

Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

35. Достаточное условие локального экстремума.

Пусть функция непрерывна ви существуют конечные или бесконечные односторонние производные. Тогда при условии

x0 является точкой строгого локального максимума. А если

то x0 является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке x0

Пусть функция f непрерывна и дважды дифференцируема в точке x0. Тогда при условии

и

x0 является точкой локального максимума. А если

и

то x0 является точкой локального минимума.

36. Определение выпуклости

За направление выпуклости отвечает знак второй производной.

Если на связанном промежутке (a,b) вторая производная >0 то выпуклость ВНИЗ, если <0 ВВЕРХ.

41. Точка перегиба.

Точка, при которой меняется направление выпуклости называется точкой перегиба.

Касательная в этой точке «протыкает» график насквозь.

Y=x³

42 Необходимое и достаточное условие перегиба

 Необходимые условия наличия перегиба

     либо не существует.

     Достаточные условия наличия перегиба

     1. Если меняет знак при переходе через точку x0, то x0 - точка перегиба.

     2. Если то при n четном x0 - точка перегиба, при n нечетном x0 не является точкой перегиба.

43 Линейные операции над векторами

Произведение вектора на число,

Деление отрезка в данном отношении.Пусть l – некоторая прямая, АВ – отрезок на l. Точка С , принадлежащая отрезку AB , делит его в отношении λ , если .

Запишем это соотношение в координатном виде :

здесь(x2,y2,z2)  - координаты точки C ,(x0,y0,z0)- координаты точки A и (x1,y1,z1) - координаты точки B. Отсюда :

,,

44.Координаты вектора.

Координаты вектора – это его проекции на ось координат.

Коэффициенты в разложении вектора по базису называются координатами этого вектора в данном базисе.

45.Координаты центра тяжести.

P1(x1,y1); P2(x2,y2); . , Pn(xn,yn) c массами m1,m2,m3, . . . , mn. Обозначим через xc и yc координаты центра тяжести данной системы материальных точек. Тогда координаты центра тяжести описанной материальной системы определяются формулами:

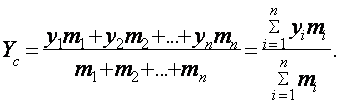
Центр тяжести тетраэдра лежит на отрезке, соединяющем вершину с точкой соединения медиан противоположной грани и делить этот отрезок в отношении 3:1 от вершины.AF=3/4AE AF=1/4(a+b+c)

Центр тяжести треугольника, указанного в условии задачи, находится в точке пересечения его медиан. Из элементарной геометрии известно, что три медианы треугольника пересекаются в одной точке, причем эта точка делит медианы в отношении 2:1, считая от вершины треугольника.