18 Вычисление производных по определению.

19. Уравнение касательной к графику функции

y=f(x₀)+f ’(x₀) * (x – x₀)

Составьте уравнение касательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как

1. a = 3 – абсцисса точки касания. 2. f(3) = – 2. 3. f '(x) = x2 – 4, f '(3) = 5. y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

21 Производная сложной функции

Производная сложной функции равна произведению производной внешней функции на производную от внутренней функции.

23 Производная показательно-степенной функции.

Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.

Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.

Найдем производную функции y = u^v. Логарифмируя, получим:

 lny = vlnu

24 Теорема Ролля.

Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

25 Теорема Лагранжа.

Формула конечных приращений

F ‘(c) = Δf/Δx (приращение функции/ приращение аргумента)

или теорема о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка , что.

Геометрически: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Физически: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение — средняяскорость за этот промежуток.

Vср=S(t2)-S(t1) / t2 – t1

26. Теорема Коши.

Пусть даны две функции итакие, что:

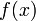1. и 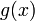определены и непрерывны на отрезке;

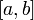2. производные 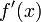и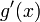конечны на интервале;

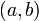3. производные 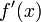и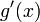не обращаются в ноль одновременно на интервале

4. ;

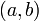
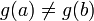тогда

, где

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а равна как раз необходимому числу.

27. Правило Лопиталя.

Метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и .

=> . н/р

28-32 Бесконечные величины.

Бесконечно малая величина

Последовательность an называется бесконечно малой, если . Например, последовательность чисел— бесконечно малая.

Функция называется бесконечно малой в окрестности точки x0, если .

Функция называется бесконечно малой на бесконечности, если либо.

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x),.

Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx, неограниченная с обеих сторон, не является бесконечно большой при .

Последовательность an называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки x0, если .

Функция называется бесконечно большой на бесконечности, если либо

Сравнение бесконечно малых

Отношение бесконечно малых величин образует так называемую неопределённость .

Определения

Допустим, у нас есть бесконечно малые при одном и том же величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).

Если , то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

Если , то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

Если (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости. Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

Если (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Примеры сравнения

При величина x5 имеет высший порядок малости относительно x3, так какС другой стороны, x3 имеет низший порядок малости относительно x5, так как

С использованием О-символики полученные результаты могут быть записаны в следующем виде x5 = o(x3).

то есть при функции f(x) = 2x2 + 6x и g(x) = x являются бесконечно малыми величинами одного порядка.

В данном случае справедливы записи 2x2 + 6x = O(x) и x = O(2x2 + 6x).

При бесконечно малая величина 2x3 имеет третий порядок малости относительно x, посколькубесконечно малая 0,7x2 — второй порядок, бесконечно малая— порядок 0,5.

Эквивалентные величины

Определение

Если , то бесконечно малые величины α и β называются эквивалентными (). Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При справедливы следующие соотношения эквивалентности (как следствия из т. н.замечательных пределов):

, где

, где

, поэтому используют выражение:

, где .