4 Бесконечные пределы

Пусть числовая функция задана на множестве , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка . В этом случае число называется пределом функции на бесконечности, если для всякой бесконечно большой последовательноститочек соответствующая последовательность частных значений функции в этих точках сходится к числу .

Пусть числовая функция задана на множестве , в котором для любого числа найдётся элемент, лежащий правее него. В этом случае число называется пределом функции на плюс бесконечности, если для всякой бесконечно большой последовательности положительных точек соответствующая последовательность частных значений функции в этих точках сходится к числу .

Пусть числовая функция задана на множестве , в котором для любого числа найдётся элемент, лежащий левее него. В этом случае число называется пределом функции на минус бесконечности, если для всякой бесконечно большой последовательности отрицательных точек соответствующая последовательность частных значений функции в этих точках сходится к числу .

5Односторонние пределы

Если у любой сходящейся к точке x₀ последовательности {x_n} все ее элементы меньше x₀, а соответствующая последовательность сходится кA₁, то число A₁ называется левым пределом функции f(x).

Обозначение: .

Если у любой сходящейся к последовательностивсе ее элементы больше, а соответствующая последовательностьсходится к, то числоназывается правым пределом функции f(x):

Обозначение: .

6 Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

7 Два варианта о пределе сложной функции

Пусть существует lim (x->x0) g(x)=y0 и существует lim (y->y0) f(y)=A, и кроме того существует проколотая окрестность точки х0, в которой g(x) <> y0. Тогда существует lim (x->x0) f(g(x)) = lim (y->y0) f(y)=A.

Сложная функция – это функция от функции

(x²)’=2x (y²)’=2y*y

8 Неопределённости

Основные виды неопределенностей: ,,,,,,.Раскрывать неопределенности позволяет:

• упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

• использование замечательных пределов;

• применение правила Лопиталя;

• использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).

9 Теорема о двух милиционерах

Если функция y = f(x) такая, что для всех x в некоторой окрестности точки a, причем функциии ψ(x) имеют одинаковый предел при, то существует предел функции y = f(x) при, равный этому же значению, то есть

10 Первый замечательный предел

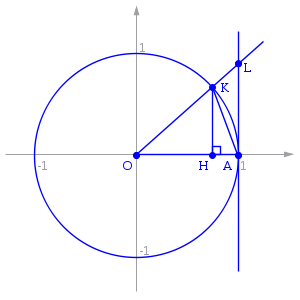
Доказательство

Рассмотрим односторонние пределыии докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(1)

(где S_sectOKA — площадь сектора OKA)

(из : |LA | = tgx)

Подставляя в (1), получим:

Так как при :

Умножаем на sinx:

Перейдём к пределу:

11Варианты первого замечательного

12 Второй замечательный предел.

Пусть . Сделаем подстановку −x = t, тогда

.

Из двух этих случаев вытекает, что для вещественного x.

13 Варианты второго замечательного.

1. 

2. 

3. 

4. 

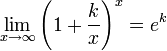
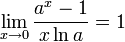5. для,

6. 

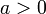14Непрерывность функции в точке.

Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.

Рациональная функция непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

16 Разрывы функций.

Точка называетсяточкой разрыва функцииy = f(x), если она принадлежит области определения функции или её границе и не является точкой непрерывности.

В этом случае говорят, что при x= x₀функция разрывна. Это может произойти, если в точкеx₀функция не определена или не существует предел, или если предел существует, но.

Функция не определена в точкеx= 0. Эта точка является точкой разрыва 1-го рода, т.к. в ней существуют пределы справа и слева.

Функция разрывна приx= 0. Действительно, приx= 0 функция не определена:.

17 Производная

Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение

Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.