3 Статистический метод расчёта электрических нагрузок в тяговой сети

3.1 Исходные данные для статистического метода расчёта тяговой сети

Исходными данными для расчёта являются тяговые нагрузки в положительной питающей линии в виде ряда случайных величин ПЛ, как показания амперметра, присоединённого через шунт в положительную питающую линию. I_ПЛ

Таблица 2. Выборка

i	1	2	3	4	5	6	7	8	9	10
IПЛ	100	120	110	90	150	200	120	100	80	100

Таблица 3- Упорядоченный статистический ряд по возрастанию

i	1	2	3	4	5	6	7
Iпл	80	90	100	110	120	150	200
ni	1	1	3	1	2	1	1
Относительная частотаW1
Эмпирическая функция распределения Fx	0,1	0,2	0,5	0,6	0,8	0,9	1

3.2 Построение гистограммы и эмпирической функции распределения

Для выборки объёмом n = 10 число интервалов, на которое разбивается статистический ряд от I_{пл min} = 80 до I_{пл max} = 200

q = 3.32lgn + 1

q = 3,32lg10+1 = 4,32 ≈ 4

Длина интервала

,

.

Подсчёт количества значений выборки, попавших в каждый интервал, учитывается так, что левая граница каждого интервала принадлежит этому интервалу, а правая – не принадлежит. Составляется таблица для построения гистограммы.

Таблица 4- Построение гистограммы

Интервал	80-110	110-140	140-170	170-200
Частота, ni	5	3	1	1
Относительная частотаW1	0,5	0,3	0,1	0,1
Плотность вероятности распределения	0,016	0,008	0,003	0,003

По данным таблицы 3 строится эмпирическая функция распределения

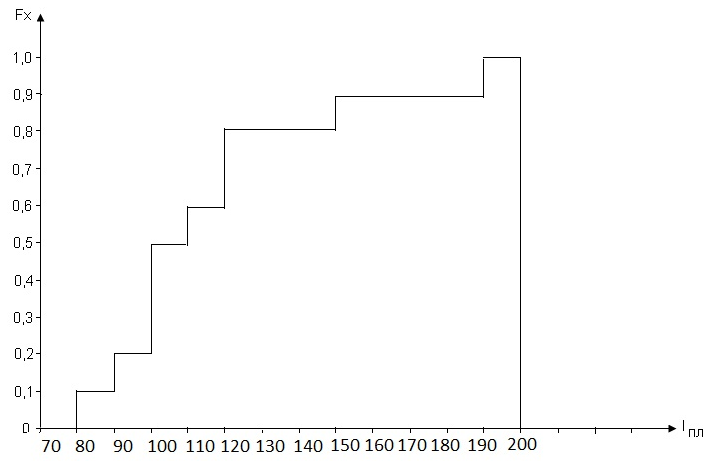
Рисунок 4 - Эмпирическая функция распределения

Рисунок 5 - Гистограмма плотности относительных частот

3.3 Определение числовых характеристик

Числовые характеристики определяются с помощью метода произведений. В качестве ложного нуля С выбирается случайная величина, расположенная примерно в центре упорядоченной выборки или случайная величина с большим значением частоты. Вариантами выступают середины интервалов, на которые разбивался ряд при построении гистограммы. Условные варианты рассчитываются по формуле

,

где h – шаг, h = 30; С = 155;

, ,

, ,

, ,

, .

Расчёты заносятся в таблицу.

Таблица 5. Расчёты методом произведений

1	2	3	4	5	6	7	8
	ni	ui	ni·ui	ni·ui2	ui + 1	( ui + 1)2	ni ( ui + 1)2
95	5	-2	-10	20	-1	1	5
125	3	-1	-3	3	0	0	0
155	1	0	0	0	1	1	1
185	1	1	1	1	2	4	4
	∑ = 10		∑ =-12	∑ = 24			∑ = 10

Для проверки вычислений:

∑ n_i·u_i² + 2 · ∑ n_i·u_i + n = ∑ n_i ( u_i + 1)²

24 + 2 · (-12) + 10 = 10

10 = 10

Вычисления в таблице выполнены верно.

Расчёт условных моментов первого и второго порядков

, ,

, .

Методом моментов рассчитываются оценки математического ожидания

– выборочного среднего Х_в, выборочной дисперсии D_в и среднеквадратично

го отклонения δ_в.

Х_в = h · + C,

Х_в = 30 · -1,2 + 155 = 119,

D_в = [ - ( )²]·h²,

D_в = [2,4 – (1,2)²]·30² = 864,

δ_в = ± ,

δ_в = ± ± 29,4.

Выборочное среднее Х_в равняется среднему току питающей линии

Х_в = I_ПЛ = 119 А.