
- •Дифференцирование функции одной переменной. Вариант 1.
- •Вариант 2.
- •Найти производную первого порядка.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
- •Вариант 21.
- •Вариант 22.
- •Найти производную первого порядка.
- •Вариант 23.
- •Вариант 24.
- •Вариант 25.
- •Вариант 26.
- •Вариант 27.
- •Вариант 28.
Вариант 9.
Найти производную первого порядка.
1.
![]() .
8.
.
8.
![]() .
.
2.
![]() .
9.
.
9.
![]() .
.
3.
![]() .
10.
.
10.
![]() .
.
4.
![]() .
11.
.
11.
![]() .
.
5.
![]() .
12.
.
12.
![]() .
.
6.
![]() .
13.
.
13.
![]() .
.
7.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
.
Найти производную второго порядка.
1.
![]() .
.
2.
![]() .
.
Найти производную третьего порядка.
![]() .
.
Найти дифференциал функции.
![]() .
.
V. Показать, что функция удовлетворяет уравнению
.
VI. Найти предельную выручку, если заданы уравнение спроса и значение цены на некоторую продукцию:
![]() ,
р=494.
,
р=494.
Вариант 10.
Найти производную первого порядка.
1.
![]() .
8.
.
.
8.
.
2.
![]() .
9.
.
9.
![]() .
.
3.
![]() .
10.
.
10.
![]() .
.
4.
![]() .
11.
.
11.
![]() .
.
5.
![]() .
12.
.
12.
![]() .
.
6.
![]() .
13.
.
13.
![]() .
.
7.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
.
Найти производную второго порядка.
1. .
2. .
Найти производную третьего порядка.
.
Найти дифференциал функции.
.
V.
Показать,
что функция
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
VI.
Издержки
производства некоторой продукции имеют
вид
![]() ,
,
Где х – число единиц продукции. Цена на этот товар составляет 36. Найти функцию прибыли и функцию предельной прибыли. Объяснить экономический смысл величины Р'(15). Вычислить и объяснить смысл величины Р(16)-Р(15).
Вариант 11.
Найти производную первого порядка.
1.
![]() .
8.
.
8.
![]() .
.
2.
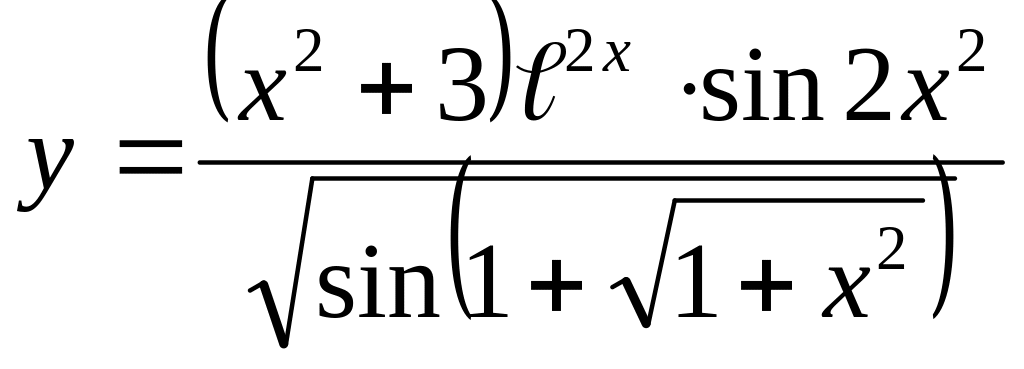 .
9.
.
9.
![]() .
.
3.
![]() .
10.
.
10.
![]() .
.
4.
![]() .
11.
.
11.
![]() .
.
5.
![]() .
12.
.
12.
![]() .
.
6.
![]() .
13.
.
13.
![]() .
.
7.
![]() .
14.
.
14.
![]() .
.
15.
![]() .
.
Найти производную второго порядка.
1.
![]() .
.
2.
![]() .
.
Найти производную третьего порядка.
![]() .
.
Найти дифференциал функции.
![]() .
.
Показать, что функция удовлетворяет уравнению
.
VI. Функция издержек производства некоторой продукции определяется следующей формулой:
![]() ,
,
где x – число единиц произведенной продукции.
Найти функцию предельных издержек, средние издержки производства x единиц продукции и скорость изменения средних издержек. При каком уровне производства скорость изменения средних издержек равна нулю?
Вариант 12.
Найти производную первого порядка.
1.
.
8.
![]() .
.
2.
![]() .
9.
.
9.
![]() .
.
3.
![]() .
10.
.
.
10.
.
4.
![]() .
11.
.
11.
![]() .
.
5.
![]() .
12.
.
12.
![]() .
.
6.
![]() .
13.
.
13.
![]() .
.
7.
.
14.
![]() .
.
15.
![]() .
.
Найти производную второго порядка.
1. .
2.
![]() .
.
Найти производную третьего порядка.
![]() .
.
Найти дифференциал функции.
![]() .
.
Показать, что функция удовлетворяет уравнению
.
VI. Функция издержек производства некоторой продукции определяется следующей формулой:
![]() ,
,
где x – число единиц произведенной продукции.
Найти функцию предельных издержек, средние издержки производства x единиц продукции и скорость изменения средних издержек. При каком уровне производства скорость изменения средних издержек равна нулю?
