1. Сущность процесса экстракции

2. Свойства треугольной диаграммы

3. Методы осуществления экстракции

4. Однократная экстракция

5. Расчёт противоточной экстракции по треугольной диаграмме

6. Расчёт противоточной экстракции по диаграмме Х-У

7. Физическая сущность абсорбции. Закон Генри

8. Основное уравнение массопередачи при абсорбции

9. Материальный баланс абсорбера

10. Тепловой баланс абсорбера

11. Абсорбция тощих газов

12. Коэффициент извлечения при абсорбции. Уравнение Кремсера

13. Принципиальная схема установки абсорбер-десорбер

14. Физическая сущность адсорбции

15. Изотерма адсорбции

16. Скорость адсорбции. Время защитного действия

17. Динамическая и статическая активность адсорбента

18. Материальный баланс адсорбера

19. Расчёт адсорбера с неподвижным адсорбентом

20. Способы регенерации адсорбентов

21. Основное уравнение гидростатики

22. Режимы движения жидкости

23. Материальный баланс потока жидкости

24. Энергетический баланс потока жидкости. Уравнение Бернулли

25. Уравнение Дарси-Вейсбаха

26. Истечение жидкости из донного отверстия при постоянном уровне

27. Истечение жидкости из донного отверстия при переменном уровне

28. Местные и линейные гидравлические сопротивления

29. Измерение скоростей и расходов жидкостей

30. Скорость осаждения в поле действия силы тяжести

31. Критериальное уравнение осаждения

32. Типы фильтрующих перегородок и осадков

33. Способы фильтрования

34. Фильтрование при постоянном перепаде давления

35. Фильтрование при постоянной скорости

36. Промывка осадка на фильтре

37. Расчёт фильтров

38. Центрифуги

39. Отстойное центрифугирование. Скорость осаждения при центрифугировании

40. Центробежное фильтрование. Движущая сила

41. Очистка газов в циклонах. Мультициклон. Гидроциклон

42. Основные характеристики псевдоожиженного слоя

43. Основные характеристики насосов

44. Схема двухкамерной печи. Полезная тепловая нагрузка печи

45. Основные характеристики печи

46. Сущность обратного цикла Карно

47. Методы искусственного охлаждения

1.Сущность процесса экстракции

Экстракция - процесс избирательного извлечения компонентов жидкой (или твердой) фазы при ее обработке р-лем, к-ый хорошо растворяет извлекаемые компоненты и ограниченно или практически не растворяет другие компоненты исходного сырья.

Применение:

• очистка смазочных масел, дизельных топлив,

• деасфальтизация тяжелых нефтяныхостатков,

• извлечение аром УВ из бензинов пиролиза, продуктов риформинга или легких газойлей коксования,

• извлечение высококипящих или нелетучих комп-ов из сточных вод.

Применяемые р-ли: фенол, фурфурол, N-метил-2-пирролидон, диэтиленгликоль, вода, жидкий пропан,бензол, диметилсульфоксид, производные морфолина и пр.

Р-р, состоящий из р-ля и извлеченных компонентов, называется экстрактным, а р-р включающий неизвлеченные компоненты и р-ль, называется рафинатным.

Извлекаемый компонент или смесь нескольких компонентов распределяется между экстрактным и рафинатным р-ми в соответствии с законом фазового равновесия:

К = х₁ / х₂,

х₁ и х₂ — концентрации извлекаемого компонента в образующихся фазах;

К — коэффициент распределения, зависящий от природы системы, состава и температуры; значение его определяется экспериментально и для данной системы он является величиной постоянной.

При выборе растворителя учитывают его избирательность (селективность) и растворяющую способность.

Повышение температуры растворения, понижение растворяющей способности растворителя и повышение его селективности достигаются добавлением в систему компонента, который хорошо растворяется в растворителе и значительно хуже — в исходной разделяемой смеси

Для повышения взаимной растворимости растворителя и исходной смеси, понижения температуры растворения и избирательности растворителя в систему добавляют компонент, хорошо растворяющийся как в растворителе, так и в исходной смеси. Скорость расслаивания определяется разностью плотностей фаз, степенью дисперсности капель и вязкостью сплошной среды.

На процесс экстракции оказывает влияние соотношение растворителя и исходного сырья. В случае небольшого количества растворителя он при соответствующей температуре полностью растворяется в исходной смеси, образуя гомогенный раствор. При большом количестве растворителя исходная смесь полностью растворяется в растворителе.

Ниже кривой растворимости находится область расслаивающихся растворов, выше — область гомогенных растворов.

t

x

2. Свойства треугольной диаграммы

В любом процессе экстракции можно выделить три составляющие: раст-ль; извлекаемый компонент, неизвлекаемый компонент.

Равносторонний ∆, вершины к-го характеризуют какое-либо аддитивное свойство чистых или обобщенных комп-ов (конц-ию, вязкость, индекс вязкости и т.п.), а каждая точка внутри треугольника отвечает трехкомпонентной системе.

С-ма сост. из трех комп-ов А, В и L, представленных вершинами равностороннего ∆-а ABL, а точка N внутри ∆-а хар-ет смесь указанных комп-ов. Массовые доли комп-ов:

; ; ;

Бинарная смесь исходных компонентов характеризуется точкой, находящейся на соответствующей стороне треугольника.

О сновные свойства треугольной диаграммы:

Первое. Если из двух с-м, хар-ых (∙) N₁, и N₂, путем смешения получают новую с-му, хар-ую (∙) N, то (∙) всех трех с-м лежат на одной прямой, к-ая (∙) N делится на части, обратно пропорциональные кол-вам комп-ов в исходных системах

Ур-ние соотв-ет прямой, проходящей через (∙) N₁, N и N₂, а (∙) N делит прямую N₁N₂ на части, обратно пропорц. массам (или объемам) исх-ых с-м (правило рычага).

А налогичным образом можно получить также следующие соотношения: g_N1/g_N2=NN2/N₁N₂, g_N2/g_N=N₁N/N₁N₂

Второе. Если при попарном смешении неск-их с-м получается одна и та же с-ма, хар-ая (∙) N, то на ∆-ой диаграмме прямые, соединяющие (∙) попарно смешиваемых систем, пересекутся в (∙) N.

Так, если попарно смешать с-мы N₁ и N₂, N₃ и N₄, к-ые обр-ют с-му N , то прямые N₁N₂ и N₃N₄ пересекутся в (∙) N. При этом справедливо следующее соотношение:

Третье. Если разность кол-в любых двух с-м есть величина пост., то на ∆-ой диаграмме прямые, проходящие через соответствующие пары (∙), хар-ие исходные с-мы, пересекутся в одной (∙) М.

Пусть имеются с-мы R₁, R₂ и R₃, к-ые при удалении из с-м S₁, S₂ и S₃ обр-ют одну и ту же с-му М.

Согласно первому св-ву можно записать: _{; ;}

Откуда

П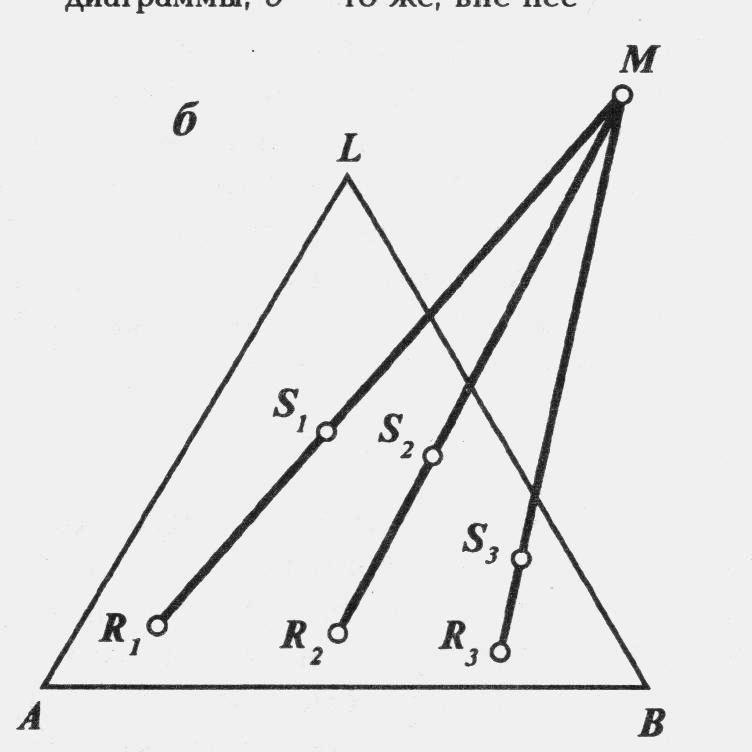 ри этом (∙) S₁, S₂ и S₃ делят соотв-ие прямые R₁М, R₂M и R₃M на части, обратно пропорциональные кол-вам соотв-их с-м, _{; ;}

(∙) пересечения М может оказаться вне ∆-ой диаграммы

Четвертое. Любая (∙), лежащая на линии LF, характеризуется постоянством соотношений комп-ов А и В. Другими словами, все р-ры исходной смеси F, состоящей из комп-ов А и В, и комп-та L, определяются (∙)-ами, лежащими на прямой LF.

Из подобия соответствующих ∆-ов следует:

Поэтому перемещение из (∙) F в (∙) N можно рассматривать как добавление к р-ру F комп-та L в соответствующих кол-вах. В соотв-вии с 1-ым св-вом все такие р-ры будут находиться на прямой LF, при этом соотношение м/у конц-ями комп-тов А и В будет оставаться неизменным и равным соотношению этих комп-тов в исходном р-ре F.Перемещение (∙) N в (∙) L будет отвечать бесконечному разбавлению исходной системы третьим компонентом L, т.е. ,а

Перемещение (∙) N по линии LF вниз соответствует постепенному удалению комп-та L из р-ра. При совмещении (∙) N с (∙) F третий комп-нт L полностью удаляется из р-ра, а смесь будет состоять только из к-тов А и В