26..Производная ф-ии и дифференциал.

Производная ф-ии – это предел отношения приращения ф-ии к приращ-ю независимой переменной при стремлении последнего к нулю (если этот предел существет).

Нахожд-е производной ф-ииназ-сядифф-ем этой ф-ии.

Если ф-я в точке х имеет конечнуюпроизв-ую, то ф-я наз-сядифф-емой в этой точке.

Ф-я, дифф-ая во всех точках промежудка, наз-сядифф-емой на этом промежутке.

Геометрич смысл: произв-ая – это тангенс угла наклона касат-й, проведенной к кривой ф-ии.

Теорема: если ф-я дифференцируема в точке , то она в этой точке непрерывна.

Дифференциал – это главная, линейная относительно ∆х, часть приращ-я ф-ии, равная произв-ю производной на приращ-е независ переем-й:

dy=f’(x)∆x.

Дифф-л независ переменной равенприращ-ю этой переменной, поэтому dy=f’(x)dx; (dx=∆x).

Инвариантность формулы дифф-ала:dy=f’(u)du. Формула не изменяется, если вместо ф-ии от независ переменной х рассматривать ф-ю от завис переменной u.

Производные и дифференциалы высших порядков.

Произв-е выше 1 порядка: f”(x), f’’’(x), 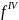(x) и т.д.

Произв-аяn-го пор-каназ-сяпроизв-ая от произво-й (n-1)-го пор-ка.

Для дифф-ия ф-ииy=f(x) использ формулу y=f’(x)dx, т.е. дифф-ал ф-ии есть ф-я от двух арг-тов х и dx. Дифф-ал 2 порядка 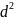у – это дифф-ал от дифф-ла первого пор-ка, т.е. у=d(dy). И у= d( у).

27.Теоремы Ферма, Ролля, Лагранжа.Без док-ва

Ферма: Если диффф-ая на промежутке Х ф-я y=f(x) достигает наибольшего /наименьшего знач-я во внутренней точке 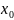этого промежутка, то производная ф-ии в этой точке равна нулю. F’( )=0.

(Геометр смысл: в точках наиб /наимзнач-я касательная к графику становится параллельна оси Ох).

Ролля: Пусть ф-я y=f(x) удовл-ет условиям: 1-непрерывна на отрезке [a;b], 2-дифф-ма на интервале (a,b), 3-на концах отрезка принимает равныезнач-я f(a)=f(b).

Тогда внутри отрезка сущ-ет по крайней мере одна такая точка E (принадл (a;b)), в которой произв-ая ф-ии равна нулю f’(E)=0.

(Геом смысл: найдется хотя бы одна точка, в кот касательная к графику ф-ии будет параллельна оси Ох)

Т Ролляявл-ся частным случаем Т Лагранжа.

Лагранжа: Пусть ф-я y=f(x) удовл условиям: 1-непрерывна на отрезке [a;b], 2-дифф-ма на интервале (a,b). Тогда внутри отрезка сущ-ет по крайней мере одна такая точка E (принадл (a;b)), в которой произв-ая равна частному от деления приращения ф-ии на приращение аргумента на этом отрезке, т.е. f’(E)=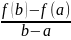 . Это можно записать в виде f(b)-f(a)= f’(E)(b-a).

Следствие: Если произв-ая ф-ииf(x) равна нулю на некотором промежутке Х, то ф-я тождественно постоянна на этом промежутке.

Коши: Если ф-ииf(x) и g(x) непрерывны на отрезке [a;b) !!!, дифф-мы на интервале (a;b) и g’(x)=0, то сущ-ет точка E (принадл (a;b)), такая, что = .

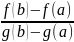Т Лагранжа явл-ся частным случаем Т Коши (при g(x)=x).

28.Точки экстремума. Необх и достаточное условия локального экстр-а ф-ии.

Т Максимума – если в некот окрестности точки выполн-сяf(x)≤f( ).

Т Минимума – если в некотокрестн-ти точки выполн-ся f(x)≥f( ).

Необхусл-е экстр-ма: Для того, чтобы ф-я y=f(x) имела экстремум в точке , необх, чтобы ее произв-ая в этой точке была равна нулю (f’( )=0) или не существовала.

Такие точки наз-сякритическими, они всегда входят в обл-тьопр-я ф-ии.

1 достатусл-е: Теорема: Если при переходе через точку произв-ая дифф-емой ф-ии y=f(x) меняет свой знак с + на --, то точка - т макс, а если с – на +, то это т мин.

2 достатусл-е: Теорема: Если первая произв-аяf’(x) дважды диффер-емой ф-ии равна нулю в некот точке , а вторая производная в этой точке f”( ) положительна, то есть т мин. Если 2-я произв-ая отрицательна, то это т макс.