
- •Матрицы и основные операции над ними. (без умножения) свойства операций?
- •2. Виды матриц. Геометрическая интерпретация векторов.
- •3. Умножение матриц. Свойства умножения матриц
- •4. Определители матриц второго и третьего порядка.
- •6. Свойства определителей.
- •7. Элементарные преобразования строк и столбцов матрицы. Их использование при нахождении определителей.
- •8. Ранг матрицы. Cпособы вычисления ранга матрицы. Геометрический смысл ранга матрицы 2 и 3 порядка?
- •9. Теорема Кронекера-Капелли о разрешимости системы линейных алгебраических уравнений.
- •11. Решение системы линейных алгебраических уравнений методом Гаусса.
- •12. Системы линейных однородных уравнений. Свойства. Фундаментальное решение.
- •13. Общее решение системы линейных алгебраических уравнений. Свободные неизвестные. Базисные решения.
- •14. Линейное пространство.Определение и пример?
- •15. Линейная зависимость и независимость векторов.?способы определения?
- •16. Базис линейного пространства. Размерность линейного пространства.
- •17. Линейные преобразования. Свойства.
- •19. Скалярное произведение векторов. Угол между векторами.
- •20. Ортонормированный базис. Евклидово пространство.
- •2 Замечат предела:
- •Признаки существования предела
- •26..Производная ф-ии и дифференциал.
- •27.Теоремы Ферма, Ролля, Лагранжа.Без док-ва
- •28.Точки экстремума. Необх и достаточное условия локального экстр-а ф-ии.
- •29.Выпуклость и точки перегиба. Необх и достатусл-я перегиба ф-ии.
- •30.Нахожд-е асимптот ф-ии.
- •Основные свойства неопределённого интеграла
- •34.Понятие определенного интеграла. Св-ва.И геометрическая интепритация пределенного интеграла
- •35.Опр интеграл как ф-я верхнего предела.
- •50. Классическое, статистическое (частное), геометрическое определение вероятности.
- •49. Независимые и зависимые событияУсловная вероятность
- •50 Формула полной вероятноститеорема Байеса
- •52. Дискретные случайные величины
- •54.Числовые характеристики дискретных случайных величин
- •56. Функция распределения случайной величины
- •59. Равномерное и нормальное распределение.
2 Замечат предела:
1)Lim
(при х->0)
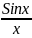 =1.
=1.
2)Lim
(при n->
к беск)
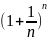 =e
(число Эйлера, прибл 2,7. иррац-ое)
=e
(число Эйлера, прибл 2,7. иррац-ое)
Основные свойства сходящихся последовательностей:
1. Сходящаяся последовательность имеет только один предел;
2. Сходящаяся последовательность ограничена;
3.
Если ![]() ,
то
,
то ![]() ;
;
4.
При любых постоянных ![]() и
и ![]()
![]() ;
;
5. ![]() ;
;
6.
Если ![]() ,
, ![]() и
и ![]() ,
то
,
то 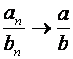 ;
;
7.
Если ![]() ,
то
,
то ![]() ;
;
8.
Если ![]() и
и ![]() ,
то
,
то ![]() ;
;
9.
Если ![]() ,
то
,
то ![]() .
.
Если последовательность не является сходящейся, то ее называют расходящейся. Расходящиеся последовательности могут быть:
1 неограниченными( бесконечно большими)
2 ограниченными(имеющими предел)
Первый замечательный предел
Рассмотрим
следующий предел: ![]() (вместо
родной буквы «хэ» я буду использовать
греческую букву «альфа», это удобнее с
точки зрения подачи материала).
(вместо
родной буквы «хэ» я буду использовать
греческую букву «альфа», это удобнее с
точки зрения подачи материала).
Согласно
нашему правилу нахождения пределов
(см. статью Пределы.
Примеры решений)
пробуем подставить ноль в функцию: в
числителе у нас получается ноль (синус
нуля равен нулю), в знаменателе, очевидно,
тоже ноль. Таким образом, мы сталкиваемся
с неопределенностью вида ![]() ,
которую, к счастью, раскрывать не нужно.
В курсе математического анализа,
доказывается, что:
,
которую, к счастью, раскрывать не нужно.
В курсе математического анализа,
доказывается, что:
![]()
Данный математический факт носит название Первого замечательного предела.
Второй замечательный предел
В теории математического анализа доказано, что:
![]()
Данный факт носит название второго замечательного предела.
Справка: ![]() –
это иррациональное число.
–
это иррациональное число.
В
качестве параметра ![]() может
выступать не только переменная
может
выступать не только переменная ![]() ,
но и сложная функция.Важно
лишь, чтобы она стремилась к бесконечности.
,
но и сложная функция.Важно
лишь, чтобы она стремилась к бесконечности.
23.Предел ф-ии в бесконечности и в точке.Свойства и признаки существования предела функции.
1.Число Аназ-ся пределом ф-ии при х -> к беск-ти, если для любого сколь угодно малого положит числа e>0 найдется такое положит число S>0, что для всех х (таких, что |x|>S), верно нерав-во:
|f(x)-A|<e.
2.Число А наз-ся пределом ф-ии при х -> к , если для любого сколь угодно малого положит числа e>0 найдется такое положит число B>0, что для всех х (не равных и удовл условию |х- |<B) соблюдается
|f(x)-A|<e.
Замечания:
1-Определение предела не требует существования ф-ии в самой точке , ибо рассматриваются значения х≠ в окрестности этой точки.
2-Если при стремлении х к переменная х принимает лишь знач-я меньше или больше , то говорят об односторонних пределах ф-ии соответственно слева (Limf(x)=A при x-> -0) и справа (Limf(x)=A при x-> +0).
свойства предела функции.
Если limx af(x) = A , то найдется окрестность точки a
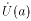 такая,
что в этой окрестности функция f(x) будет
ограничена.
такая,
что в этой окрестности функция f(x) будет
ограничена.Если f(x) есть постоянная A в некоторой окрестности точки a, то limx af(x) = A
Если limx af(x) = A1 и limx af(x) = A2, то A1 = A2
Признаки существования предела
Теорема
1 (теорема
о двух милиционерах). Если
функция y=f(x) в
некоторой окрестности точки а заключена
между двумя функциями ![]() и
и ![]() ,
т.е. выполняется неравенство
,
т.е. выполняется неравенство ![]() х,
причем эти функции имеют одинаковый
предел при
х,
причем эти функции имеют одинаковый
предел при![]() ,
то существует предел
функции y=f(x) при
,
равный этому же значению.
,
то существует предел
функции y=f(x) при
,
равный этому же значению.
![]() ,
,
![]()
![]() =>
=> ![]() .
.
2. Если функция y=f(x) монотонно возрастет (убывает) в некоторой окрестности точки а и ограничена сверху (снизу), то она имеет предел при .
24-25.Непрерывность ф-ии действ переем-й в точке и на отрезке. Св-ва ф-ий, непр на отрезке.
1.Ф-я непрерывна в точке , если она удовл трем условиям: 1-определена в точке (существует f( )), 2-имеет конечный предел ф-ии при x -> , 3-этот предел = знач-ю ф-ии в точке .
1.2.Ф-я непрерывна в точке , если она определена в этой точке, и бесконечно малому приращ-ю аргумента соответствует беск малое приращ-е ф-ии.
Св-ва ф-ий, непр в точке:
1-Если ф-ииf(x) и ⱷ(x) непрерывны в точке , то их сумма, произв-е и частное тоже непр в этой точке.
2-Если ф-я непр в точке и f( )>0, то сущ такая окрестность точки , в которой f(x)>0.
3-Если
ф-я y=f(u)
непрерывна в точке
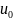 ,
а ф-я y=ⱷ(x)
непрерывна в точке
=ⱷ(
),
то сложная ф-я y=f[ⱷ(x)]
непр в точке
.
,
а ф-я y=ⱷ(x)
непрерывна в точке
=ⱷ(
),
то сложная ф-я y=f[ⱷ(x)]
непр в точке
.
2.Ф-яназ-ся непрерывной на отрезке Х, если она непрерывна в каждой точке этого отрезка.
Можно доказать, что все элементарные ф-ии непрерывны в обл-ти их определения.
Св-ва ф-ий, непр на отрезке:
1-Если ф-я непрерывна на отрезке [a;b], то она ограничена на этом отрезке (первая теорема Вайерштрасса).
2-Если ф-я непрерывна на отрезке [a;b], то она достигает на этом отр-кенаименьшзнач-я m и наибольшзнач-я M (вторая т. Вайерштрасса).
3-Если ф-я непрерывна на отрезке [a;b] и знач-я на ее концах имеют противоп знаки, то внутри отрезка найдется такая точка (E принадлежит (a;b)), что f(E)=0 (теорема Больцано - Коши).
