17. Линейные преобразования. Свойства.

Ортогональные операторы

Линейный оператор называется ортогональным, если

Для того чтобы оператор был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.

Ортогональные операторы и только они сохраняют длину вектора, т. е.

Сопряженные операторы

Оператор называется сопряженным линейному оператору , если

Оператор также является линейным оператором. Еслиfв некотором ортогональном базисе имеет матрицуA, то в этом базисе оператор имеет матрицу .

Свойства сопряженных операторов: (f- невырожденный).

Самосопряженные операторы

Линейный оператор называется самосопряженным (симметрическим), если

Для самосопряженного оператора

Оператор является самосопряженным тогда и только тогда, когда его матрица в некотором ортонормированном базисе симметрическая.

Свойства самосопряженных операторов: 1) самосопряженный оператор имеет только действительные собственные числа; 2) всякий самосопряженный оператор является оператором простой структуры; 3) для всякого самосопряженного оператора существует ортонормированный базис, состоящий из собственных векторов этого оператора.

18. Нахождение матрицы линейного преобразования.

Пусть вn- мерном линейном пространстве с базисом , ,…, задано линейное преобразование А. Тогда векторы А ,А ,…,А - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

A = a₁₁ + a₂₁ +…+ a_n1

A = a₁₂ + a₂₂ +…+ a_n2

……………………………….

A =a_n1 +a_n2 +…+a_nn

Тогда матрица А = называетсяматрицей линейного преобразования А.

Если в пространствеLвзять вектор , тоA ÎL.

,где

……………………………..

Эти равенства можно назвать линейным преобразованием в базисе , ,…, .

В матричном виде:

, А× ,

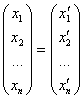19. Скалярное произведение векторов. Угол между векторами.

Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:

ab = |a||b| cosφ .

Обозначения скалярного произведения: ab, (ab), a·b .

Свойства скалярного произведения:

1. ab = |a|пр_аb.

Доказательство. По свойству проекции пр_аb = |b| cosφ, следовательно, ab = |a|пр_аb.

2. ab = 0 a b.

3. ab = ba .

4. (ka)b = k(ab).

5. (a + b)c = ac + bc .

6. a² = aa = |a|² , где а² называется скалярным квадратом вектора а.

7. Если векторы а и b определены своими декартовыми координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂},

то ab= X₁X₂ + Y₁Y₂ + Z₁Z₂.

Доказательство. Используя формулу, получим:

ab= (X₁i + Y₁j + Z₁k)(X₂i + Y₂j + Z₂k) .

Используя свойства 4 и 5, раскроем скобки в правой части полученного равенства:

ab= X₁X₂ii +Y₁Y₂jj + Z₁Z₂kk + X₁Y₂ij +X₁Z₂ik + Y₁X₂ji+ Y₁Z₂jk + Z₁X₂ki + Z₁Y₂kj.

Но ii = jj = kk = 1 по свойству 6, ij = ji = ik = ki = jk = kj= 0 по свойству 2, поэтому

ab= X₁X₂ + Y₁Y₂ + Z₁Z₂ .

Угол между векторами:

cosφ= .

20. Ортонормированный базис. Евклидово пространство.

Если векторыe_1,e₂,e₃попарно перпендикулярны и длина каждого из них равна единице, то базис называетсяортонормированным, а координаты x₁, x₂, x₃-прямоугольными.Базисные векторы ортонормированного базиса будем обозначатьi, j, k.

Будем предполагать, что в пространствеR³выбрана правая система декартовых прямоугольных координат {0,i, j, k}.

Ортонормированная система, состоящая изnвекторовn-мерного евклидова пространства, образует базис этого пространства. Такой базис называетсяортонормированнымбазисом.

Еслиe₁,e₂,..., e_n—ортонормированныйбазисn-мерного евклидова пространства и

x=x₁e₁+x₂e₂+ ... +x_ne_n— разложение вектораxпо этому базису, то координатыx_iвектораxв ортонормированном базисе вычисляются по формуламx_i=(x, e_i),i= 1, 2, ...,n.

Евклидово пространство(такжеЭвклидово пространство) — в изначальном смысле, пространство свойства которого описываются аксиомамиевклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.

22.Предел числпосл-ти. Признаки существования предела..Основные свойства сходящихся последователь­ностей. Расходящиеся последовательности.

Два замечательных предела.

Число А – предел числпосл-ти{ }, если для любого (сколь угодно малого) положит числа найдется такой номер N, что для всех членов посл-ти с номерами n>N верно неравенство | -A|<∑. Если посл-ть имеет предел, то она – сходящаяся, если не имеет, то расх.

Признаки сущ-я предела:

1-Если числпосл-ть{ } монотонна и ограниченна, то она имеет предел.

2-Если в некот окрестности точки (или при достаточно больших знач-ях х) ф-я f(x) заключена между другими двумя (фи от икс и трезубец от икс), имеющими одинаковый предел А, то ф-я f(x) имеет тот же предел А.