13. Общее решение системы линейных алгебраических уравнений. Свободные неизвестные. Базисные решения.

Рассмотрим однородную линейную систему

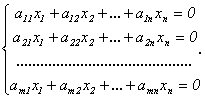
Отметим, что такая система всегда совместна, поскольку имеет нулевое решение называемое тривиальным.

Пусть ранг матрицы системыr<n. Предположим, что в базисный минор входят коэффициенты первыхrуравнений. Тогда оставшиесяm–rуравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первыеrуравнений:

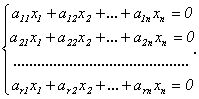
Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:

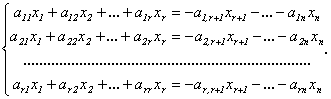
Эта система будет иметь единственное решение относительно неизвестных выражающее их через остальные неизвестные ( ), которым можно придавать любые произвольные значения. Таким образом, система приr<nявляется неопределенной.

Неизвестные коэффициенты при которых входят в базисный минор матрицы системы, называютсябазисными неизвестными, а остальные ( ) –свободными неизвестными.

Решения системы 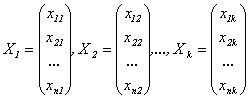называютсялинейно независимыми, если линейная комбинация дает нулевой столбец только при

14. Линейное пространство.Определение и пример?

ПустьV- непустое множество (его элементы будем называть векторами и обозначать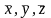 ...), в котором установлены правила:

1) любым двум элементам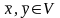 соответствует третий элемент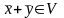 , называемый суммой элементов (внутренняя операция);

2) каждому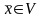 и каждому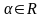 отвечает определенный элемент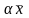 (внешняя операция).

МножествоVназывается действительным линейным (векторным) пространством, если выполняются аксиомы:

I. ,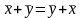

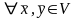
II. ,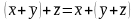

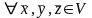
III.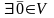 (нулевой элемент, такой, что , ).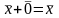

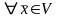IV. 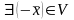(элемент, противоположный элементу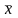 ), такой, что .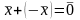

V. , .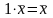

VI. , ,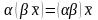

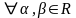
VII. , ,

VIII. , ,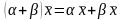

Пример. Рассмотрим множество M ⁿ многочленов с действительными коэффициентами относительно одного переменного, n-й степени, n>1, с определенными для многочленов операциями сложения и умножения на число.

M ⁿ = {P_n| P_n (t) = a_ntⁿ + a_n-1t ⁿ-1 + … + a₁t + a₀, a_n не равно 0}

Это множество не является линейным пространством.

Действительно., рассмотрим P_n = t ⁿ + t и Q_n = - t ⁿ. Оба эти многочлена принадлежат множеству. Однако их сумма,  P_n + Q_n = (t ⁿ + t) + (- t ⁿ) = -t,

Не принадлежит M ⁿ, поскольку -t — многочлен первой степени, а множество M ⁿ содержит многочлены n-й степени,  n >1.

15. Линейная зависимость и независимость векторов.?способы определения?

Систе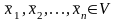ма линейно зависима 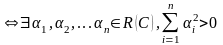, что .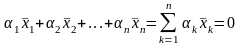

Система линейно независима .

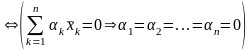Критерий линейной зависимости векторов

Для того чтобы векторы 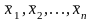(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

16. Базис линейного пространства. Размерность линейного пространства.

Базисом линейного пространстваLназывается такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов.

В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

Линейное пространствоL, в котором существует базис, состоящий изnвекторов, называетсяn-мерным линейным иливекторным пространством. Числоnназываетсяразмерностьюпространства и обозначаетсяdimL. Линейное пространство, в котором не существует базис, называетсябесконечномерным.