9. Теорема Кронекера-Капелли о разрешимости системы линейных алгебраических уравнений.

Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA=RgA^*.

Очевидно, что система может быть записана в виде:

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А А^*не изменяют ранга.

2) ЕслиRgA=RgA^*, то это означает, что они имеют один и тот жебазисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, т.е. верна запись, приведенная выше.

11. Решение системы линейных алгебраических уравнений методом Гаусса.

Метод Гаусса называют методом последовательного исключения неизвестных. Сущность метода заключается в том, что при помощи элементарных преобразований, таких как умножения (деления) любого уравнения системы на число и сложения с любым другим уравнением система приводится к треугольному виду. Последнее уравнение позволяет сделать заключение о совместности системы и, если система определенна, найти одно из неизвестных. Затем, двигаясь от последнего уравнения к первому (операции обратного хода), последовательно определяются все неизвестные системы.

Рассмотрим алгоритм метода Гаусса на примере решения системы уравнений.

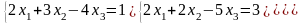
В рассматриваемом примере коэффициенты при всех неизвестных отличны от единицы. Сделаем первое уравнение ведущим для исключения переменной х₁, для чего все уравнение разделим на коэффициент при х₁, который равен 2.

Ведущее уравнение запишем первым в системе

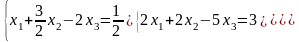
Из системы уравнений видно, что для исключения неизвестной х₁ из второго уравнения нужно первое уравнение умножить на (-2) и сложить со вторым. Для исключения неизвестной х₁ из третьего уравнения нужно первое уравнение умножить на (-4) и сложить с третьим.

В результате этих операций система уравнений будет иметь вид:

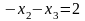
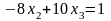
Теперь за ведущее примем второе уравнение и исключим неизвестную х₂ из третьего уравнения. Для этого второе уравнение нужно умножить на (-8) и сложить с третьим.

Будем иметь систему уравнений

Это были операции прямого хода. В результате исключения неизвестных х₁ и х₂ получена система треугольного вида.

Операции обратного хода.

Из последнего уравнения определяется ;

Из второго уравнения определяется ;

Из первого уравнения определяется .

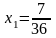12. Системы линейных однородных уравнений. Свойства. Фундаментальное решение.

В общем виде система n линейных однородных алгебраических уравнений запишется

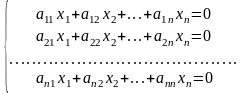
Очевидно, такая система имеет нулевое (тривиальное) решение

Если ∆ ≠ 0, то такая система имеет единственное решение, корни которого . Других ненулевых решений нет.

Если ∆ = 0, то так как все вспомогательные определители системы равны нулю, то система имеет бесконечное множество решений.

Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

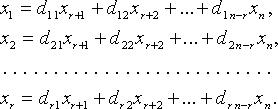
Тогдаn - rлинейно независимыми вектор-решениями будут:

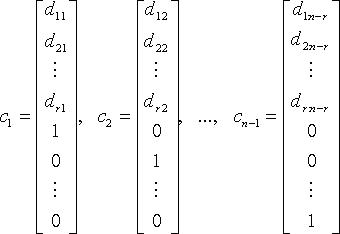
а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.