54.Числовые характеристики дискретных случайных величин

Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

где –возможные значения случайной величины Х , а – соответствующие вероятности.

Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу:

причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства.

Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

52. Определение случайной величины. Дискретные и непрерывные случайные величины.Непрерывные случайные величины

Функцией распределения вероятностей называют функцию , определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х , то есть:

Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку (а,б), называют определенный интеграл

Если возможные значения принадлежат всей числовой оси, то

(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные непрерывной случайной величины Х принадлежат отрезку(а,б) , то

Если возможные значения принадлежат всей числовой оси, то

(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).

Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:

56. Функция распределения случайной величины

Если x - дискретная случайная величина, принимающая значения x1 < x2 < … <xi< … с вероятностями p1 < p2 < … <pi< …, то таблица вида

X1	X2	…	xi	…..
P1	P2	…	P1	…..

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид

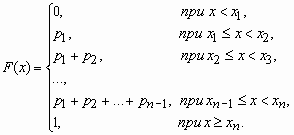
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1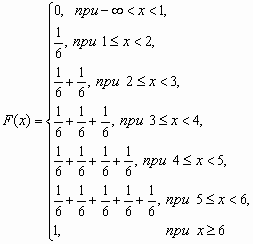 2 3 4 5 6

1/6 1/6 1/6 1/6 1/6 1/6

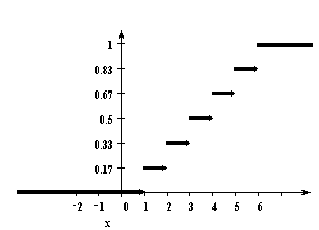
54. Числовые характеристики случайных величин: математическое ожидание, мода, медиана. Свойства математического ожидания.

Математическое ожидание случайной величины. Свойства математического ожидания. Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение

 

x1	x2	...	xn
p1	p2	...	pn

называется величина  , если число значений случайной величины конечно.

Если число значений случайной величины счетно, то  . При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_x(x) вычисляется по формуле 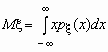 . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x , h = f(x), то

.

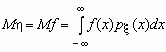Аналогичные формулы справедливы для функций дискретной случайной величины:

,  .

Основные свойства математического ожидания:

• математическое ожидание константы равно этой константе, Mc=c ;

• математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );

• математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

54.Числовые характеристики случайных величин: дисперсия, среднее квадратическое отклонение. Их свойства.

Дисперсия случайной величины. Свойства Дисперсии. Диспе́рсияслуча́йной величины́ — мера разброса данной случайной величины, т. е. её отклонения отматематического ожидания. Обозначается  Свойства: 1. Дисперсия любой случайной величины неотрицательна:  2. Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; 3. Если случайная величина равна константе, то её дисперсия равна нулю:   Верно и обратное: если   то   почти всюду; 4. Дисперсия суммы двух случайных величин равна:

, где   — их ковариация;

5. Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

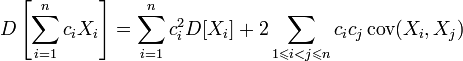, где  ; В частности,   для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;

6. 7. 8.