49. Независимые и зависимые событияУсловная вероятность

Условной вероятностью события А при условии того, что произошло событие В, называют величину: , из чего следует, что: . При этом, следует читать как Р(В) или Р(А) соответственно, индекс – лишь обозначение условной вероятности.

50 Формула полной вероятноститеорема Байеса

Предположим, что событие   может осуществляться только с одним из несовместных событий  . Например, в магазин поступает одна и та же продукция от трех предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие  ). Здесь события  — это выбор изделия из продукции соответствующего предприятия.

В этом случае вероятность события   можно рассматривать как сумму произведений событий

По теореме сложения вероятностей несовместных событий получаем

Используя теорему умножения вероятностей, находим

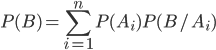 (3.1)

Формула (3.1) носит название формулы полной вероятности.

Пример. Для рассмотренного выше случая с поступлением товара в магазин от трех предприятий зададим численные значения. Пусть от первого предприятия поступило 20 изделий, от второго — 10 изделий и от третьего — 70 изделий. Вероятности некачественного изготовления изделия на предприятиях соответственно равны 0,02; 0,03 и 0,05.

Определить вероятность взятия некачественного изделия.

Решение. Вероятности событий  будут равны P(А₁) = 0,2; P(А₂) = 0,1; P(А₃) = 0,7. Используя формулу (3.1), находим

P(B) = 0,2×0,02 + 0,1×0,03 + 0,7×0,05 = 0,042.

Формула Байеса (теорема гипотез)

Пусть событие А может наступить лишь при условии появления одного из несовместных событий В1,В2…,Вn образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами.

Допустим, что произведено испытание, в результате которого появилось событие A . Выясним, как изменятся вероятности гипотез в связи с тем, что событие A уже наступило, то есть найдем условные вероятности .

Для произвольной гипотезы Bi ( ) в силу определения произведения двух событий справедливо равенство , но по теореме о вероятности совместного появления двух событий получим:

,

Следовательно

Выразим из последней формулы и затем заменим по формуле полной вероятности:

,

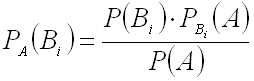
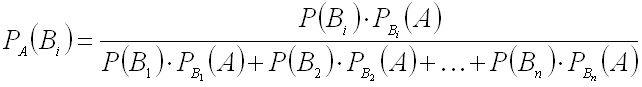
Полученное выражение для гипотез Bi ( ) называют формулами Байеса.

Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие A

52. Дискретные случайные величины

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

55.Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.