1. Матрицы и основные операции над ними. (без умножения) свойства операций?

Матрицей будем называть таблицу размером m´n, которая содержит m строк и n столбцов. Матрицу записываем в виде

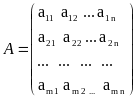
Операции над матрицами.

Транспонированием матрицы называется операция, при которой меняются местами строки и столбцы матрицы. Обозначается:

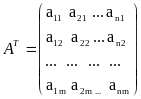
Умножением матрицы на число называется операция, при которой каждый элемент новой матрицы равен произведению элемента данной матрицы на данное число. То есть:

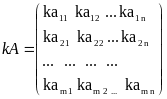
Суммой двух матриц называется операция, при которой каждый элемент новой матрицы равен сумме элементов данных матриц. То есть:

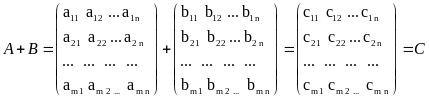
Произведением двух матриц A и B называется операция, при которой каждый элемент новой матрицы C равен:

Операция сложения матриц обладает следующими свойствами: для любых матриц   и нулевой матрицы 

1) A+B=B+A; (перестановочность или коммутативность операции сложения

2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)

3) A+O = O+A =A;

4) A+(-A)=(-A)+A=O.

2. Виды матриц. Геометрическая интерпретация векторов.

Матрица, содержащая только одну строку или один столбец, называется вектор строкой или вектор столбцом.

Матрица, все элементы которой равны 0, называется нулевой.

Матрица, все элементы главной диагонали которой не равны нулю, а все остальные элементы равны нулю, называется диагональной, то есть:

.

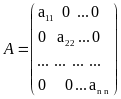Матрица, число строк и число столбцов которой равны, называется квадратной (в противном случае прямоугольной).

В случае если все элементы главной диагонали матрицы равны 1, а остальные 0, то матрица называется единичной:

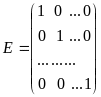
Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N-мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x =(x1, x2,...,xN)t можно изобразить точкой в этом пространстве с координатами (x1, x2,...,xN).

3. Умножение матриц. Свойства умножения матриц

Пусть даны две матрицы 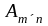и 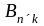, таких что число столбцов матрицы А равно числу строк матрицы В . Тогда произведением матриц и называется матрица ,каждый элемент которой Cij равен сумме попарных произведений элементов i-той строки матрицы А на соответствующие элементы j-того столбца матрицы В, т.е.

Пример умножения матриц:

Операции умножения матрицы на число обладаtт следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А - А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С - матрицы, α и β - числа.

4. Определители матриц второго и третьего порядка.

Каждой квадратной матрице ставится в соответствие число, обозначаемое

Рассмотрим определители для матриц второго и третьего порядков:

Пусть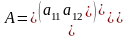 ,тогда

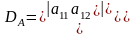
Из формулы следует, что определитель для матрицы второго порядка равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.

Пусть 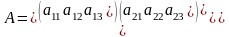, тогда

Существуют различные правила, позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.

Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2 .

схема 1 схема 2

5. Обратная матрица и её нахождение.

Алгебраическим дополнением элемента а_ij квадратной матрицы называется число А_ij,вычисляемое по формуле:

где M_ij-определитель полученный из определителя матрицы 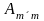удалением строки с номером i и столбца с номером j .

Матрица А^-1 называется обратной к матрице А, если

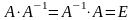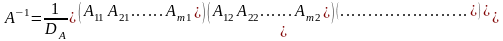,гдеЕ - единичная матрица. Из определения следует, что матрицыА и А^-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от нуля и , где А_ij-алгебраические дополнения элемента а_ij матрицы .