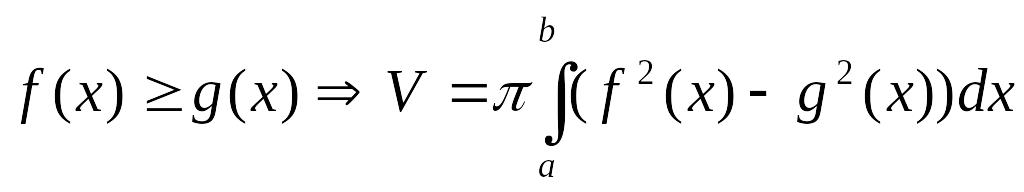1. Понятие несобственного интеграла первого рода и его вычисление

Пусть функция непрерывна на промежутке .

Несобственный интеграл первого рода от функции определяется как предел обычного определенного интеграла:

Если предел в правой части существует и конечен, то несобственный интеграл 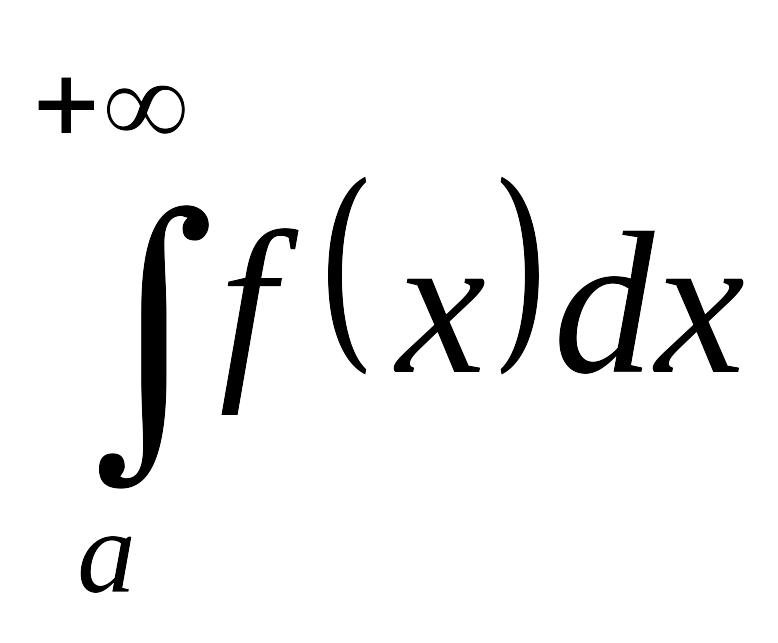называется сходящимся, а функция интегрируемой на бесконечном промежутке ; если же предел не существует или бесконечен, то говорят, что интеграл расходится.

Аналогично определяется несобственный интеграл на промежутке

Несобственный интеграл с двумя бесконечными пределами определяется формулой

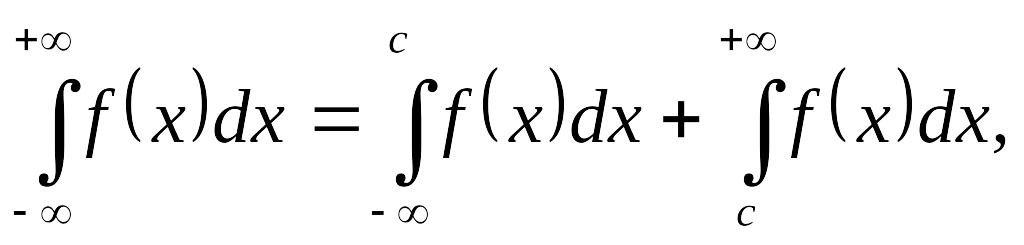
где с – произвольное число.

Г еометрическим смыслом сходящегося несобственного интеграла первого рода является площадь криволинейной трапеции с бесконечно длинным основанием (рис. 37)

Рис. 37

Пример….Исследовать сходимость где

Решение.

а) если то а значит

Мы вычислили значение интеграла, а значит доказали его сходимость.

б) если то а значит

Следовательно, искомый интеграл расходится.

в) если то

что доказывает расходимость интеграла.

2. Понятие несобственного интеграла второго рода

Для функции непрерывной на промежутке и терпящей бесконечный разрыв в точке несобственным интегралом второго рода от функции на промежутке называется интеграл:

Если предел в правой части существует и конечен, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.

Аналогично определяется несобственный интеграл на промежутке функции терпящей бесконечный разрыв в точке

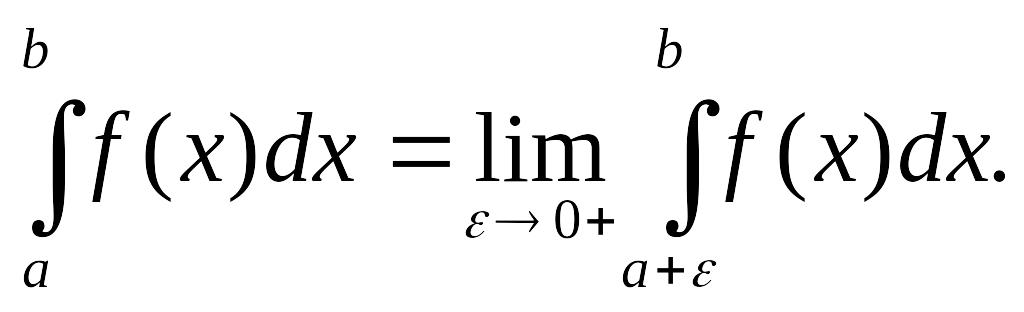
Если функция терпит бесконечный разрыв во внутренней точке с отрезка то несобственным интегралом второго рода от функции , которая имеет бесконечный разрыв во внутренней точке , определяется, как сумма несобственных интегралов второго рода по его частям и

Данный интеграл будет сходящимся только в том случае, если оба интеграла в правой части сходятся.

Геометрическим смыслом сходящегося несобственного интеграла второго рода является площадь бесконечно высокой криволинейной трапеции (рис. 38).

Рис.38

Пример 8.13. Исследовать на сходимость интеграл

Решение. Подынтегральная функция имеет разрыв второго рода в точке Поэтому,

Следовательно, интеграл расходится.

3. Приложения определенного интеграла

Рассмотрим несколько основных приложений определенного интеграла.

Вычисление площади плоской фигуры в декартовой системе координат

№	Рисунок	Формула
1	Криволинейная трапеция ограничена сверху графиком функции , снизу осью , слева и справа прямыми и
2	Криволинейная трапеция ограничена снизу графиком функции , сверху осью , слева и справа прямыми и
3	К риволинейная трапеция ограничена кривой , которая конечное число раз меняет знак на осью и прямыми и
4	К риволинейная трапеция ограничена сверху графиком функции , снизу графиком функции , слева и справа прямыми и

Пример.. Вычислить площадь фигуры, ограниченной линиями:

а) б)

Решение.

а ) Построим фигуру, площадь которой требуется найти (рис. 39).

Кривая является параболой с вершиной в точке Парабола пересекает ось в точках и Фигура состоит из двух частей, следовательно

Рис. 39

б ) Для построения фигуры, площадь которой требуется найти, найдем точки пересечения параболы и прямой Решим СЛАУ:

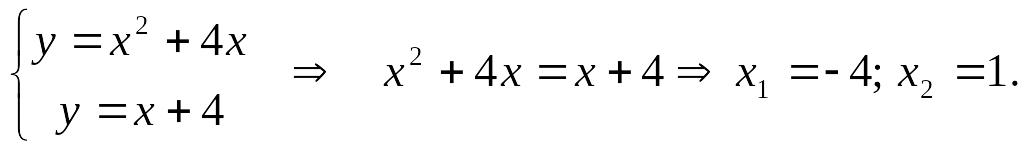
Построим прямую и параболу с вершиной и точками пересечения оси в и Строим прямую и параболу (рис. 40)

Рис. 40

Имеем,

Вычисление длины дуги кривой

Если функция непрерывна вместе с на отрезке то длина дуги кривой АВ выражается формулой

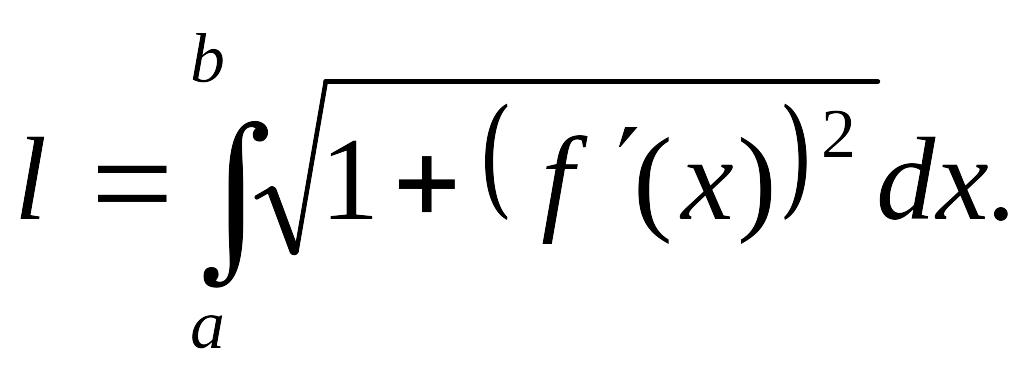
Пример. Найти длину дуги полукубической параболы от точки до точки

Решение. Полукубическая парабола симметрична относительно оси (см. рис….). Точки и лежат на верхней ветви параболы, которая описывается уравнением Тогда и по формуле имеем:

Вычисление объема тела вращения

№	Рисунок	Формула
1	Тело образовано вращением вокруг оси криволинейной трапеции, ограниченной сверху графиком функции , снизу осью , слева и справа прямыми и
2	…. Тело образовано вращением вокруг оси криволинейной трапеции, ограниченной сверху графиком функции , снизу графиком функции , слева и справа прямыми и