Понятие определенного интеграла и его свойства
Пусть на отрезке
задана непрерывная функция
причем
для определенности
1) Разобьем отрезок
на оси
точками
на n произвольных частичных отрезков
Означим через
длину
наибольшего частичного отрезка разбиения:
где
2) В каждом из полученных частичных отрезков выберем произвольную точку и
3) составим сумму
Данная сумма
называется интегральной
суммой для
функции
на отрезке
4) Если существует
конечный предел I
интегральной суммы при
не зависящий ни от способа разбиения
отрезка
,
ни от выбора точек
внутри каждого отрезка, то этот предел
называют определенным
интегралом
от функции
по отрезку
и обозначается:
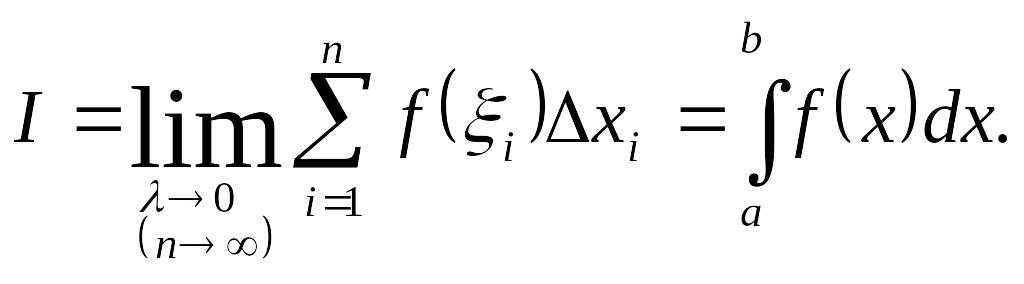
Функция
называется подынтегральной
функцией, выражение
подынтегральным выражением, числа
и
называются соответственно нижним
и верхним
пределами интегрирования,
переменной
интегрирования.
Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на нем.
Теорема 2. Если функция кусочно-непрерывна на отрезке , то она интегрируема на нем.
Таким образом, возвращаясь к рассмотренным выше задачам, получаем:
- масса неоднородного стержня длины l вычисляется по формуле
где
функция
плотности;
- путь, пройденный неравномерно двигающейся точкой за время от до вычисляется по формуле
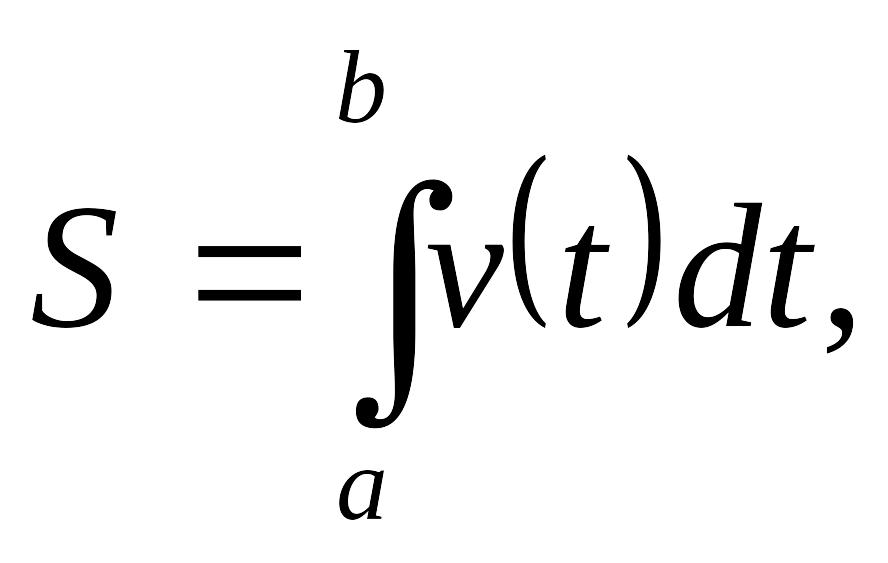
где
функция
скорости.
Геометрическая интерпретация определенного интеграла
Пусть на отрезке
задана непрерывная функция
,
причем
на
.
Криволинейной
трапецией
называется фигура, ограниченная осью
,
прямыми
и графиком функции
.
Найдем площадь криволинейной трапеции.
1) Разобьем отрезок на оси точками
на n произвольных частичных отрезков
Означим через длину наибольшего частичного отрезка разбиения: где
2) В каждом из полученных частичных отрезков выберем произвольную точку и
3) составим сумму
Интегральная сумма
равна площади ступенчатой фигуры,
состоящей из прямоугольников, вписанных
в криволинейную трапецию (рис. 36)
Рис. 36
Площадью криволинейной
трапеции считают предел площадей
ступенчатых фигур, получаемых при
неограниченном увеличении n
числа точек дробления отрезка
и при условии, что
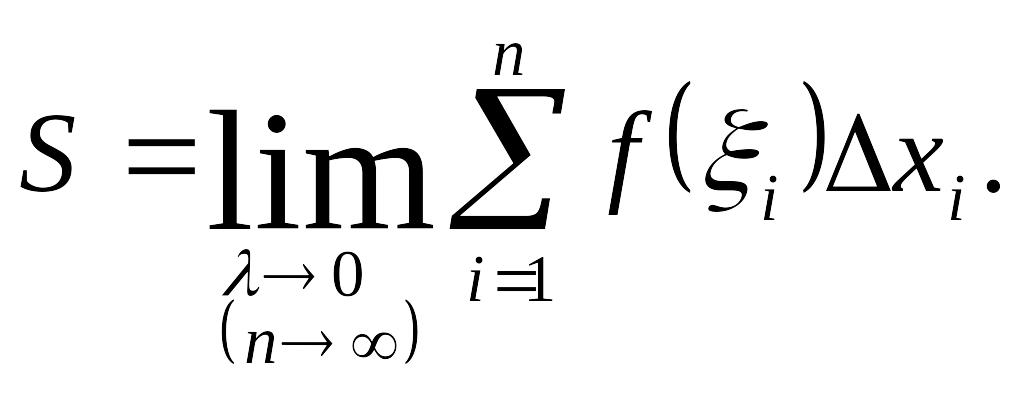
Таким образом,
геометрически
интеграл от непрерывной неотрицательной
на отрезке
функции
есть площадь криволинейной трапеции,
ограниченной линиями
осью
и графиком функции
:
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла, другие справедливы только для него.
Основные свойства определенного интеграла
Будем считать, что функция непрерывна на .
1. Интеграл с одинаковыми пределами интегрирования равен нулю:
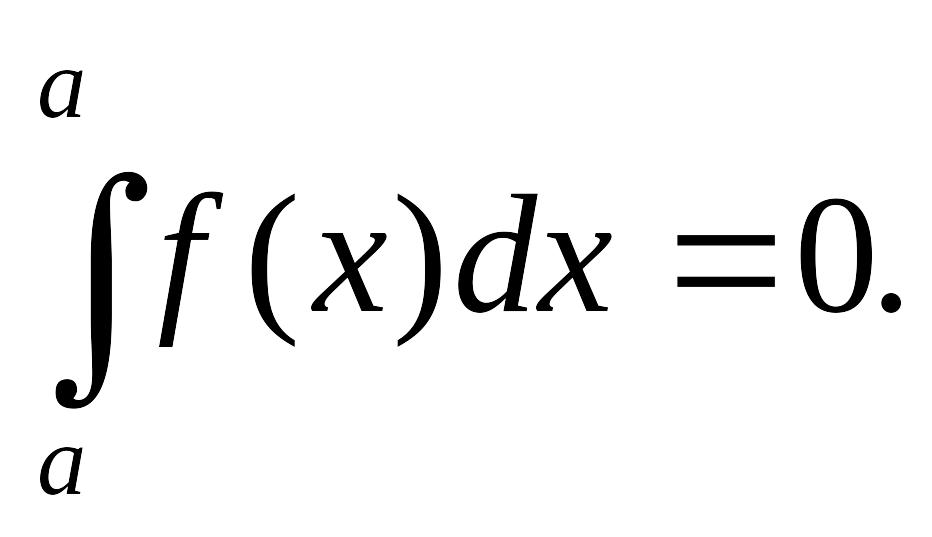
2.
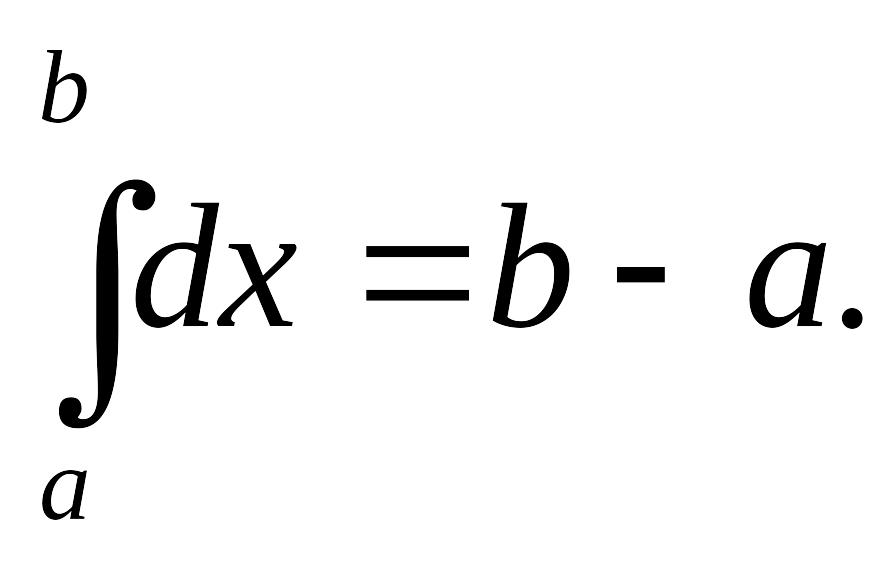
3. При перестановке
местами пределов интегрирования
определенный интеграл меняет свой знак
на противоположный:
4. Интеграл по
отрезку равен сумме интегралов по его
частям, т.е. имеет место равенство:
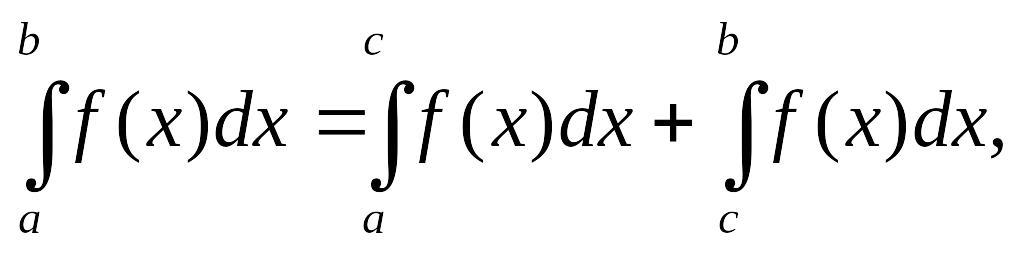если
5. Постоянный
множитель можно выносить за знак
определенного интеграла:
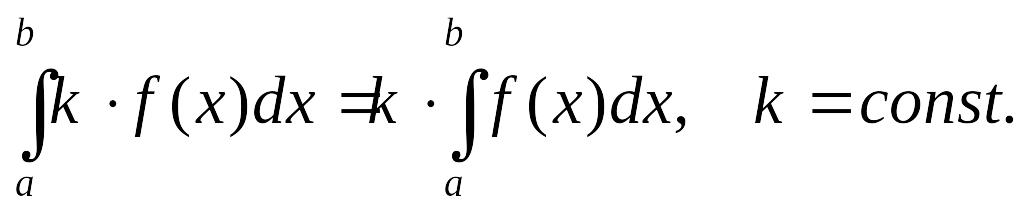
6. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых, т.е. (для двух функций):
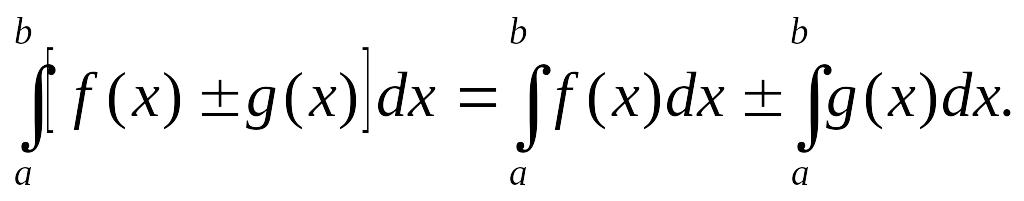
7. Теорема
о среднем.
Если
непрерывна на
,
то существует такое число
что
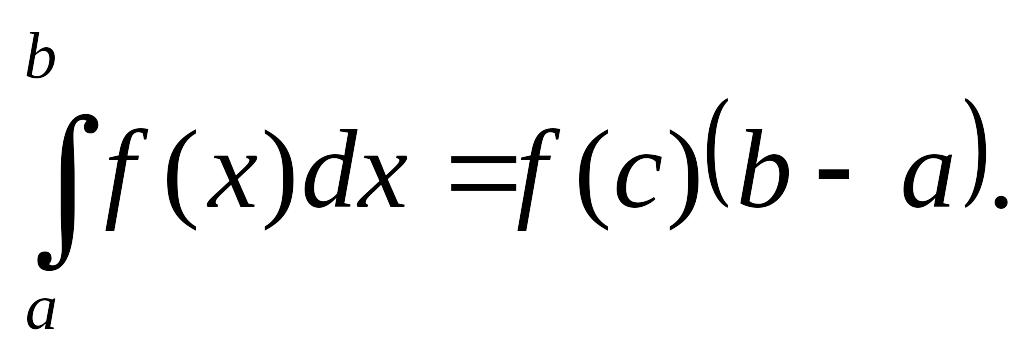
8. Определенный интеграл зависит только от вида функции и пределов интегрирования, но не от переменной интегрирования, которую можно обозначить любой буквой:
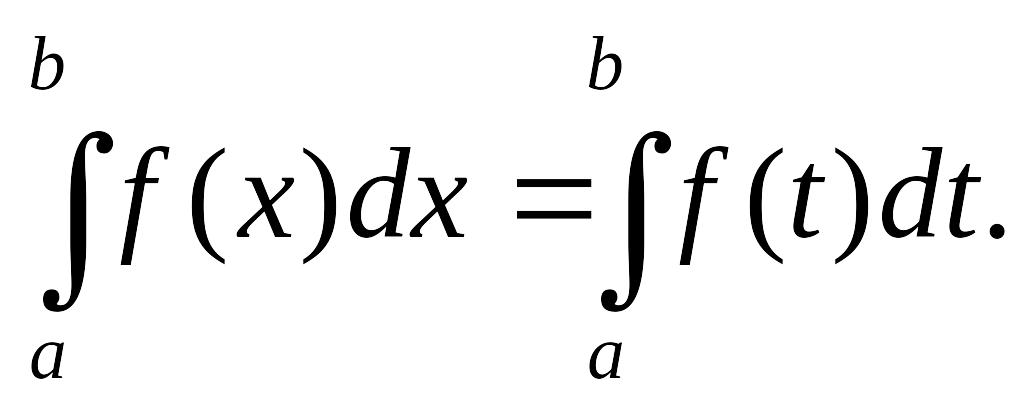
Вычисление определенного интеграла как предела интегральной суммы неудобно и трудоемко. Поэтому целесообразно указать более удобный и эффективный способ вычисления определенного интеграла. Основан он на связи неопределенного и определенного интеграла и выражается в формуле Ньютона-Лейбница.