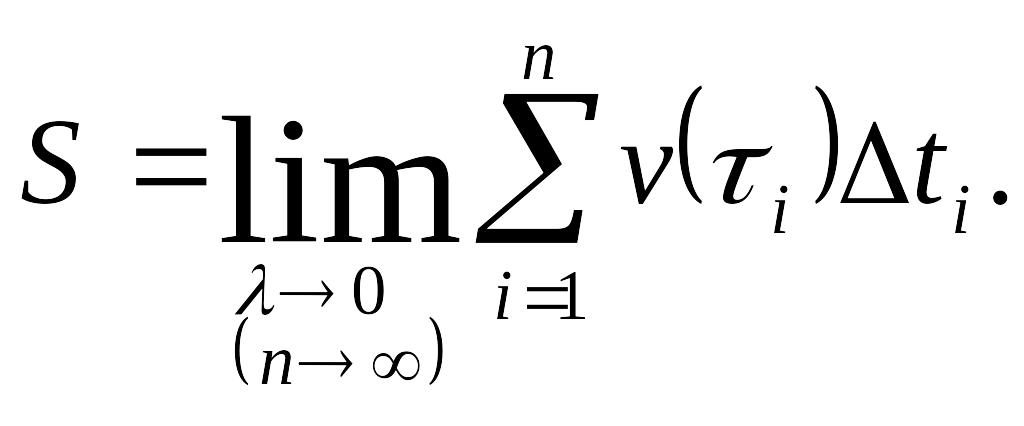2. Интегрирование некоторых тригонометрических функций

1. Интегралы вида можно свести к табличным, применяя:

а) формулы понижения степени

в случае, если и неотрицательные четные числа.

Пример. Вычислить интеграл

Решение. Здесь

б) подстановку , если или нечетные числа.

Допустим, для определенности, что нечетное Тогда,

Полученный интеграл стал табличным.

Пример.. Вычислить интеграл

Решение. Здесь и имеет место подстановка Тогда

2. Интегралы вида

С помощью замены переменной которая называется универсальной тригонометрической подстановкой, данный интеграл всегда сводиться к интегралу от рациональной функции. При такой замене имеем

Тогда,

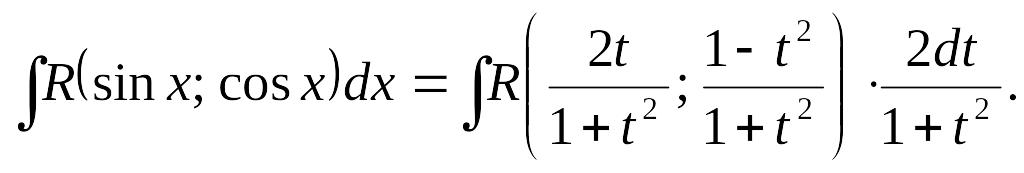
Пример… Вычислить интеграл

Решение. Произведем универсальную тригонометрическую подстановку. Получим

3. «Неберущиеся» интегралы

К настоящему времени разработано множество методов интегрирования. Мы рассмотрели лишь некоторые из них. Интеграл от элементарной функции который сам является элементарной функцией, называют «берущимся». Оказывается, что берущихся интегралов мало на фоне всех интегралов. Большинство интегралов являются «неберущимися», то есть не представимыми через элементарные функции, Так, например, нельзя взять интеграл , так как не существует элементарной функции, производная от которой была бы равна Приведем примеры «неберущих» интегралов:

интеграл Пуассона;

интегральный логарифм и экспонента;

интегралы Френеля;

интегральный синус и косинус;

Неберущиеся интегралы имеют богатую историю и многочисленные практические приложения. Интеграл Пуассона, например, описывает один из важнейших законов теории вероятности, а интегралы Френеля применяются в физике.

Лекция 8.3. Определенный интеграл и его вычисление

План:

1. Задачи, приводящие к понятию определенного интеграла.

2. Понятие определенного интеграла и его свойства.

3. Формула Ньютона-Лейбница и основные методы нахождения определенного интеграла.

Интегралы, рассмотренные ранее, носили название неопределенных. Само название указывает, что в нем какая-то величина должна быть неопределенна. И это постоянная С, которая могла принимать любое числовое значении.

Определенному интегралу в математическом анализе отводится особое место в связи с его практической значимостью. Так, к вычислению определенного интеграла сводится решение задач по нахождению площадей, длин и объемов тел, работы, скорости движущего тела и т.д.

Существенное отличие определенного интеграла от неопределенного заключается в том, что определенный интеграл выражается некоторым числом. Однако между этими интегралами есть много общего.

1. Задачи, приводящие к понятию определенного интеграла

Задача о массе стержня

Зная длину стержня и его плотность для любого найти его массу

Решение. Если стержень однородный, то есть то

Пусть стержень неоднородный, т.е. Выполним следующие действия:

1) Разобьем стержень точками

на n произвольных частичных отрезков

Означим через длину наибольшего частичного отрезка разбиения: где длина го отрезка.

2) В каждом из полученных частичных отрезков выберем произвольную точку и положим, что на отрезке плотность постоянна и равна

3) Массу го отрезка вычислим приближенно

4) Тогда масса всего стержня приближенно равна

Это приближенное равенство тем точнее, чем меньше значение Будем производить разбиение стержня на части таким образом, чтобы (а тогда ). Тогда

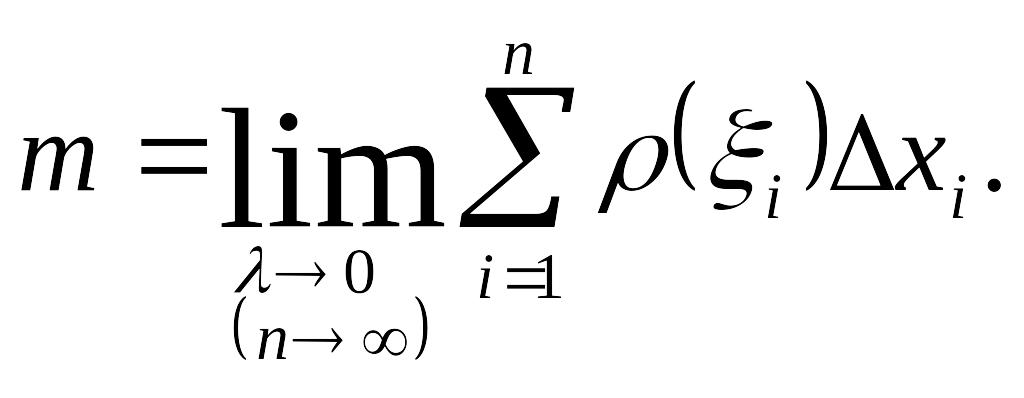
Задача о пройденном пути

Зная промежуток времени от до и функцию скорости движения точки в момент времени найти путь пройденный точкой M.

Решение. Если бы точка M двигалась равномерно, то есть то

Пусть движение неравномерное и скорость есть непрерывная функция, т.е. Выполним следующие действия:

1) Разобьем промежуток времени точками

на n произвольных частичных отрезков

Означим через длину наибольшего частичного отрезка разбиения:

где длина го отрезка.

2) В каждом из полученных частичных отрезков выберем произвольную точку и будем считать, что за этот промежуток времени происходит равномерное движение со скоростью

3) Путь , пройденный точкой M за промежуток времени приближенно равен

4) Тогда путь S, пройденный за время от до приближенно равен

Это приближенное равенство тем точнее, чем меньше Устремляя (а тогда ), в пределе получим