1. Интегрирование рациональных функций

Рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочленов

где постоянные коэффициенты.

Дробь называется правильной, если степень ее числителя меньше степени ее знаменателя, т.е. в противном случае дробь называется неправильной.

Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби. Для этого надо разделить числитель на знаменатель по правилу деления многочленов "столбиком».

Например,

Поскольку интегрирование многочлена не составляет никаких трудностей, то задача интегрирования произвольной рациональной дроби сводится к задаче интегрирования правильной рациональной дроби.

Разложение правильной рациональной дроби на простейшие

Простейшими дробями называются правильные рациональные дроби вида:

I. II.

III. , т.е. квадратный трехчлен не имеет корней.

IV.

где действительные числа.

Теорема… Всякая правильная рациональная дробь может быть представлена в виде суммы простейших дробей.

Например,

где действительные числа, неопределенные (пока!) числа, которые нужно найти (их называют неопределенными коэффициентами). В общем случае число простейших дробей, соответствующих множителю , стоящему в знаменателе, равно k.

Пример. Запишите формулу разложения правильной рациональной дроби на простейшие: а) б) в)

Решение.

а)

б)

в)

Каким образом находятся коэффициенты в разложении правильной дроби на простейшие?

Для нахождения неопределенных коэффициентов применяют или «метод сравнения коэффициентов» или «метод отдельных значений коэффициентов».

Алгоритм методов

	Метод сравнения коэффициентов	Метод отдельных значений коэффициентов
1	Приведем к общему знаменателю слагаемые правой части разложения; получим тождество где многочлен с неопределенными коэффициентами;
2	Приравняем числители т.к. знаменатели равны;
3	Приравняем коэффициенты при одинаковых степенях Получим СЛАУ, из которой найдем искомые коэффициенты.	Придадим конкретные значения столько раз, сколько неопределенных коэффициентов (обычно вместо полагают значения действительных корней многочлена

Пример. Разложить дробь на простейшие

Решение. По теореме разложим дробь на простейшие:

Найдем коэффициенты «методом отдельных значений коэффициентов»:

1)

2)

3) Пусть тогда т.е.

Пусть тогда т.е.

Пусть тогда т.е.

Следовательно,

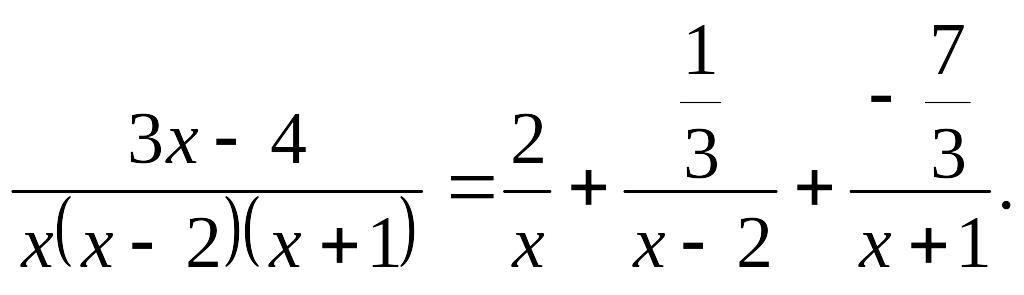
Интегрирование простейших дробей

Правило интегрирования рациональных дробей

1. Выделяем целую часть, если дробь неправильная.

2. Находим нули знаменателя

3. Разлагаем знаменатель на линейные множители, соответствующие действительным корням и квадратные трехчлены, соответствующие комплексным корням.

4. Разлагаем правильную дробь на сумму простейших дробей.

5. Интегрируем целую часть (если она есть) и простейшие дроби.

6. Складываем полученные интегралы.

Пример.. Вычислить интеграл

Решение. 1) Выделим целую часть данной неправильной дроби

2) Разложим знаменатель на линейные множители по формуле где и корни квадратного уравнения, то есть

Найдем и «методом сравнения коэффициентов»:

Значит, разложение правильной дроби в виде суммы простейших дробей имеет вид:

3)