Тема 8. Интегральное исчисление
Лекция 8.1. Первообразная и неопределенный интеграл
План:
1. Определение первообразной и неопределенного интеграла
2. Непосредственное интегрирование
3. Основные методы интегрирования
Из школьного курса известно, что для каждого математического действия существует ему обратное, то есть сделанные друг за другом, уничтожают результаты друг друга, а число, к которому они последовательно были применены, остается неизменным. Это вычитание и сложение, умножение и деление, возведение в степень и извлечение корня, логарифмирование – потенцированию, дифференцирование – интегрирование.
Например, если
известен закон
прямолинейного
движения материальной точки, выражающий
зависимость пути s
от времени t,
то скорость точки находится как
производная пути по времени:
.
Однако может возникнуть и обратная
задача: по известной скорости прямолинейного
движения точки
,
найти закон движения
.
Ясно, что искомая функция будет такая,
для которой
.
Интеграл (от лат. integer – целый), одно из самых важных понятий математики, появившееся в связи с возникшей потребностью, с одной стороны, находить функции по их производным, а с другой – находить площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п
1. Определение первообразной и неопределенного интеграла
Функция
называется первообразной
для функции
на некотором промежутке
,
если для любого
выполняется
равенство:
.
Из определения ясно, что функция должна быть непрерывна на всем промежутке и дифференцируема во всех внутренних точках данного промежутка.
Пример.
Найти первообразную для функции
.
Решение.
Первообразной будет функция
,
т.к.
.
Однако, первообразной будут и функции
и
и
,
которые отличаются только величиной
слагаемого. В силу того, что производная
постоянной равна нулю, имеем
.
Следовательно, любая функция вида
,
где С
– произвольная постоянная, будет
первообразной для данной функции.
Возникает вопрос:
исчерпывается ли множество всех
первообразных для данной функции
выражением вида
,
где
– одна из
первообразных, С
– произвольная
постоянная.
Теорема 7.1.
(об общем виде первообразной)
Две различные первообразные
и
одной и той же функции
,
определенной на промежутке
,
отличаются друг от друга на постоянное
слагаемое, т.е.
Доказательство.
Пусть функция
и
являются первообразными для функции
.
Тогда выполняются равенства:
и
.
Рассмотрим производную разности
Тогда разность этих двух первообразных
тождественно равна константе, т.е.
.
Теорема доказана.
Эта теорема позволяет ввести понятие неопределенного интеграла.
Неопределенным
интегралом от функции
на промежутке
называется
совокупность всех первообразных для
функции
на этом промежутке и обозначается
символом
где
знак
интеграла;
переменная
интегрирования;
подынтегральная
функция;
подынтегральное
выражение.
Процесс нахождения неопределенного интеграла называют интегрированием.
Итак,
Возвращаясь к
рассмотренному примеру, можем записать
так
как
Приведем еще несколько примеров:
так
как
так
как
так как
С геометрической точки зрения неопределенный интеграл – это некоторое семейство кривых, определяющих одну из первообразных и отличающихся на постоянную величину.
Свойства неопределенного интеграла
Будем считать, что все рассматриваемые функции определены на промежутке , функция непрерывна на и дифференцируема во всех внутренних точках .
1. Производная от
неопределенного интеграла равна
подыитегральной функции, т.е.
Доказательство.
2. Дифференциал от
неопределенного интеграла равен
подынтегральному выражению, т.е.
Доказательство. По определению дифференциала имеем:
3. Интеграл от
дифференциала некоторой функции равен
сумме этой функции и произвольной
постоянной, т.е.
Доказательство.
По определению дифференциала и
определению неопределенного интеграла
имеем
4. Неопределенный
интеграл от алгебраической суммы функций
равен алгебраической суме интегралов
от слагаемых, т.е. (для двух функций)
Доказательство.
Пусть
и
.
Тогда
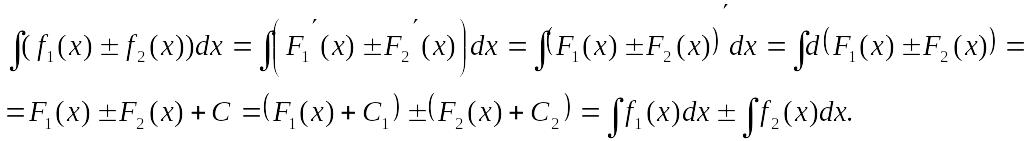
5. Постоянный
множитель можно выносить за знак
интеграла, т.е. для
выполнено
Доказательство.
По свойству
имеем
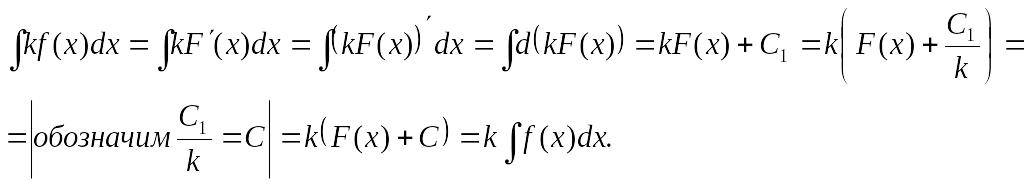
6. Если
то
где
произвольная
дифференцируемая функция. Это свойство
называется свойство
инвариантности формул интегрирования.